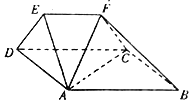
题目内容
【题目】设 ![]() 为椭圆
为椭圆 ![]() 上任一点,
上任一点,![]() ,
,![]() 为椭圆的焦点,
为椭圆的焦点,![]() ,离心率为
,离心率为 ![]() .
.
(1)求椭圆的标准方程;
(2)直线 ![]() 经过点
经过点 ![]() ,且与椭圆交于
,且与椭圆交于 ![]() ,
,![]() 两点,若直线
两点,若直线 ![]() ,
,![]() ,
,![]() 的斜率依次成等比数列,求直线
的斜率依次成等比数列,求直线 ![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 或
或 ![]() .
.
【解析】试题分析:(1)由,![]() ,运用椭圆的定义可得
,运用椭圆的定义可得![]() ,由离心率公式可得
,由离心率公式可得![]() ,再由
,再由![]() 的关系可得
的关系可得![]() ,从而得到椭圆方程;(2)由直线
,从而得到椭圆方程;(2)由直线 ![]() 经过点
经过点 ![]() ,可知,
,可知,![]() ,设点
,设点 ![]() ,
,![]() ,由
,由 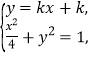 消
消 ![]() ,得
,得 ![]() ,利用韦达定理和等比中项的性质,化简整理可得
,利用韦达定理和等比中项的性质,化简整理可得![]() 的值,进而得到所求直线方程.
的值,进而得到所求直线方程.
试题解析:(1) 由椭圆的定义可得 ![]() ,可得
,可得 ![]() ,
,
由 ![]() ,可得
,可得 ![]() ,
,![]() ,
,
则椭圆方程为 ![]() ;
;
(2) 由直线 ![]() 经过点
经过点 ![]() ,可知,
,可知,![]() ,
,
设点 ![]() ,
,![]() ,
,
由 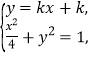 消
消 ![]() ,得
,得 ![]() ,
,
由直线与椭圆交于不同的两点,可得 ![]() ,解得
,解得 ![]() ,
,
由韦达定理得,![]() ,
,![]() ,
,
由题意知,![]() ,
,
即
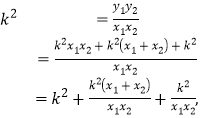
所以 ![]() ,即
,即 ![]() ,
,
即 ![]() ,即为
,即为 ![]() ,
,
所以直线 ![]() 的方程为
的方程为 ![]() 或
或 ![]() .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案【题目】某市电力公司为了制定节电方案,需要了解居民用电情况,通过随机抽样,电力公司获得了![]() 户居民的月平均用电量,分为六组制出频率分布表和频率分布直方图(如图所示).
户居民的月平均用电量,分为六组制出频率分布表和频率分布直方图(如图所示).
组号 | 分组 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(1)求![]() ,
, ![]() 的值;
的值;
(2)为了解用电量较大的用户用电情况,在第![]() 、
、![]() 两组用分层抽样的方法选取
两组用分层抽样的方法选取![]() 户.
户.
①求第![]() 、
、![]() 两组各取多少户?
两组各取多少户?
②若再从这![]() 户中随机选出
户中随机选出![]() 户进行入户了解用电情况,求这
户进行入户了解用电情况,求这![]() 户中至少有一户月平均用电量在
户中至少有一户月平均用电量在![]() 范围内的概率.
范围内的概率.
【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况,随机抽查了该市60名网友在该网店的网购金额情况,如表:
网购金额 (单位:千元) | 频数 | 频率 |
| 3 |
|
|
|
|
| 9 |
|
| 15 |
|
| 18 |
|
|
|
|
合计 | 60 |
|
若将当日网购金额不小于2千元的网友称为“网购达人”,网购金额小于2千元的网友称为“网购探者”,已知“网购达人”与“网购探者”人数的比例为![]() .
.
(1)确定![]() ,
,![]() ,
,![]() ,
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;

(2)试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数;若平均数和中位数至少有一个不低于2千元,则该网店当日评为“皇冠店”,试判断该网店当日能否被评为“皇冠店”.