题目内容
7.已知函数f(x)=log2|x|.(1)判断函数f(x)的奇偶性,并证明;
(2)根据函数奇偶性判断f(x)在(-∞,0)上的单调性,并说明理由.
分析 (1)首先判断还是的定义域,然后判断f(-x)与f(x)的关系;
(2)首先判断还是在(0,+∞)的单调性,然后利用奇偶性判断(-∞,0)上的单调性.
解答 解:(1)是偶函数;
证明:函数的定义域为{x|x≠0},
f(-x)=log2|-x|=log2|x|=f(x),所以函数f(x)是偶函数;
(2)函数f(x)=log2x在(0,+∞)是增函数,由根据偶函数对称区间的单调性相反,得到函数在(-∞,0)是减函数.
点评 本题考查了函数奇偶性的判断以及偶函数对称区间的单调性相反.属于基础题.

练习册系列答案
相关题目
18.在平行六面体ABCD-A1B1C1D1中,若AA1=AB=AD=1,∠A1AD=∠A1AB=∠BAD=60°,则直线AC1与平面ABCD所成的角的余弦值为( )
| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
12.复数z满足(1+i)z=3+i,则复数z在复平面内所对应的点的坐标是( )
| A. | (1,-2) | B. | (-2,1) | C. | (-1,2) | D. | (2,-1) |
17.已知某几何体的三视图如图所示,则该几何体的体积为( )
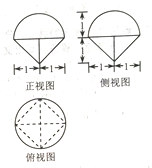

| A. | $\frac{2}{3}({π+1})$ | B. | $\frac{4}{3}$(π+1) | C. | $\frac{4}{3}$(π+$\frac{1}{2}$) | D. | $\frac{2}{3}$(π+$\frac{1}{2}$) |