题目内容
19.已知点A(1,1),B(2,3),C(0,2),D(5,5)则向量$\overrightarrow{AC}$在$\overrightarrow{BD}$方向上的投影为-$\frac{\sqrt{13}}{13}$.分析 设向量$\overrightarrow{AC}$与$\overrightarrow{BD}$的夹角为θ,由条件求得cosθ=$\frac{\overrightarrow{AC}•\overrightarrow{BD}}{|\overrightarrow{AC}|•|\overrightarrow{BD}|}$ 的值,再根据向量$\overrightarrow{AC}$在$\overrightarrow{BD}$方向上的投影为|$\overrightarrow{AC}$|•cosθ,计算求得结果.
解答 解:由题意可得向量$\overrightarrow{AC}$=(-1,1),$\overrightarrow{BD}$=(3,2),∴|$\overrightarrow{AC}$|=$\sqrt{2}$,|$\overrightarrow{BD}$|=$\sqrt{9+4}$=$\sqrt{13}$.
设向量$\overrightarrow{AC}$与$\overrightarrow{BD}$的夹角为θ,则cosθ=$\frac{\overrightarrow{AC}•\overrightarrow{BD}}{|\overrightarrow{AC}|•|\overrightarrow{BD}|}$=$\frac{-3+2}{\sqrt{2}•\sqrt{13}}$=-$\frac{1}{\sqrt{26}}$.
故向量$\overrightarrow{AC}$在$\overrightarrow{BD}$方向上的投影为|$\overrightarrow{AC}$|•cosθ=-$\frac{\sqrt{2}}{\sqrt{26}}$=-$\frac{\sqrt{13}}{13}$,
故答案为:-$\frac{\sqrt{13}}{13}$.
点评 本题主要考查两个向量的数量积的运算,求一个向量在另一个向量上的投影,属于基础题.

| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
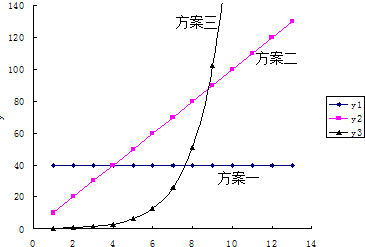
| A. | 投资3天以内(含3天),采用方案一 | B. | 投资4天,不采用方案三 | ||
| C. | 投资6天,采用方案二 | D. | 投资10天,采用方案二 |