题目内容
20.已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{19}$,则|$\overrightarrow{a}$-$\overrightarrow{b}$|等于( )| A. | $\sqrt{13}$ | B. | $\sqrt{15}$ | C. | $\sqrt{17}$ | D. | $\sqrt{7}$ |
分析 |$\overrightarrow{a}$+$\overrightarrow{b}$|2═$\overrightarrow{a}$2$+\overrightarrow{b}$2+2$\overrightarrow{a}$$•\overrightarrow{b}$,整体求解2$•\overrightarrow{a}$$•\overrightarrow{b}$=6,运用|$\overrightarrow{a}$-$\overrightarrow{b}$|2=$\overrightarrow{a}$2$+\overrightarrow{b}$2$-2\overrightarrow{a}$$•\overrightarrow{b}$,得出|$\overrightarrow{a}$-$\overrightarrow{b}$|
解答 解:∵$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{19}$,
∴2$•\overrightarrow{a}$$•\overrightarrow{b}$=6,
∵|$\overrightarrow{a}$-$\overrightarrow{b}$|2=$\overrightarrow{a}$2$+\overrightarrow{b}$2$-2\overrightarrow{a}$$•\overrightarrow{b}$=4+9-6=7,
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{7}$,
故选:D.
点评 本题考查了平面向量的运算,关键是运用好向量的平方和向量模的平方的关系,属于容易题.

| A. | 1 | B. | i | C. | -1 | D. | -i |
| A. | -360 | B. | 360 | C. | -60 | D. | 60 |
| A. | 必要而不充分条件 | B. | 充分而不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | y=3x-2 | B. | y=x+1 | C. | y=2x-1 | D. | y=-2x+3 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
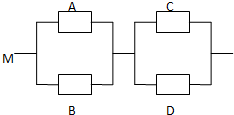 如图,用A、B、C、D表示四类不同的元件连接成系统M.当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时,系统M正常工作.已知元件A、B、C、D正常工作的概率依次为:0.3、0.6、0.5、0.8,元件连接成的系统M正常工作的概率P(M)=0.648.
如图,用A、B、C、D表示四类不同的元件连接成系统M.当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时,系统M正常工作.已知元件A、B、C、D正常工作的概率依次为:0.3、0.6、0.5、0.8,元件连接成的系统M正常工作的概率P(M)=0.648.