题目内容
【题目】如图,正方形![]() 所在平面与等腰梯形
所在平面与等腰梯形![]() 所在平面互相垂直,已知
所在平面互相垂直,已知![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)分别证明BD垂直DE和AD,结合直线与平面垂直判定,即可.(2)建立坐标系,分别计算两个平面的法向量,结合向量数量积公式,即可.
证明:(1)因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
由余弦定理可得![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)因为四边形![]() 是等腰梯形,
是等腰梯形,![]() ,
,
又由(1)知![]() ,所以
,所以![]() ,所以
,所以![]() .
.
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线作为
所在直线作为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的坐标系,
轴建立如图所示的坐标系,
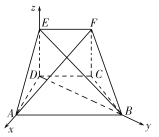
设![]() ,则
,则![]() ,可得
,可得![]() ,
,![]() ,
,
由![]() ,
,![]() ,可得,
,可得,![]() ,
,
由此可得![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则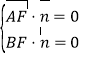 ,
,
可得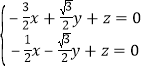 ,
,
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,
由(1)知,![]() ,
,![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
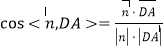
![]() .
.
所以所求锐二面角的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】为大力提倡“厉行节约,反对浪费”,某市通过随机调查100名性别不同的居民是否做到“光盘”行动,得到如下列联表:
| 做不到“光盘”行动 | 做到“光盘”行动 |
男 | 45 | 10 |
女 | 30 | 15 |
经计算 . 附表:
. 附表:
|
|
|
|
|
|
|
|
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过![]() 的前提下,认为“该市居民能否做到
的前提下,认为“该市居民能否做到![]() 光盘
光盘![]() 行动与性别有关”
行动与性别有关”
![]() 的前提下,认为“该市居民能否做到
的前提下,认为“该市居民能否做到![]() 光盘
光盘![]() 行动与性别无关”
行动与性别无关”
C.有![]() 以上的把握认为“该市居民能否做到
以上的把握认为“该市居民能否做到![]() 光盘
光盘![]() 行动与性别有关”
行动与性别有关”
D.有![]() 以上的把握认为“该市居民能否做到
以上的把握认为“该市居民能否做到![]() 光盘
光盘![]() 行动与性别无关”
行动与性别无关”