题目内容
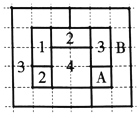
【题目】在正方体
中，
是棱
的中点，
是侧面
内的动点,且
与平面
的垂线垂直，如图所示，下列说法不正确的序号为__________
①点的轨迹是一条线段.②与
是异面直线.
③与
不可能平行.④三棱锥
的体积为定值.
【答案】③
【解析】
分别根据线面平行的性质定理以及异面直线的定义，以及体积公式分别进行判断.
对于①，设平面
与直线
交于点
，连接
，则为的中点..
分别取
的中点
，连接
，
则
平面
，
平面.
所以
平面，同理可得
平面
是平面
内的相交直线.
所以平面
平面，
由
与平面的垂线垂直,则
平面，可得直线
平面.
即点
是线段
上的动点，所以①正确.
对于②，由①有点在线段上，所以
三点在侧面
内.
假设与
不是异面直线，则
四点共面,则他们共面于侧面内.
这与在正方体中，显然
产生矛盾，所以假设不成立.
故与是异面直线，故②正确.
对于③，当与
重合时，
，所以③错误.
对于④，
,
,则平面
.
则点到平面的距离等于点(或点
)到平面的距离.
设点(或点)到平面的距离为
.
则
，即
.
在正方体中，
，
，
均为定值，所以为定值.
点到平面的距离为定值，又为定值.
所以
的体积为定值,故④正确.
故答案为：③.
【题目】[2019·潍坊期末]某钢铁加工厂新生产一批钢管，为了了解这批产品的质量状况，检验员随机抽取了100件钢管作为样本进行检测，将它们的内径尺寸作为质量指标值，由检测结果得如下频率分布表和频率分布直方图：
分组 | 频数 | 频率 |
25.05～25.15 | 2 | 0.02 |
25.15～25.25 | ||
25.25～25.35 | 18 | |
25.35～25.45 | ||
25.45～25.55 | ||
25.55～25.65 | 10 | 0.1 |
25.65～25.75 | 3 | 0.03 |
合计 | 100 | 1 |
（1）求
，
；
（2）根据质量标准规定：钢管内径尺寸大于等于25.75或小于25.15为不合格，钢管尺寸在
或
为合格等级，钢管尺寸在
为优秀等级，钢管的检测费用为0.5元/根．
（i）若从
和
的5件样品中随机抽取2根，求至少有一根钢管为合格的概率；
（ii）若这批钢管共有2000根，把样本的频率作为这批钢管的频率，有两种销售方案：
①对该批剩余钢管不再进行检测，所有钢管均以45元/根售出；
②对该批剩余钢管一一进行检测，不合格产品不销售，合格等级的钢管50元/根，优等钢管60元/根．
请你为该企业选择最好的销售方案，并说明理由．
【题目】某种新产品投放市场一段时间后，经过调研获得了时间
（天数）与销售单价
（元）的一组数据，且做了一定的数据处理（如表），并作出了散点图（如图）
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中
，
.
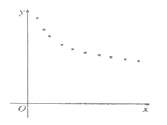
（1）根据散点图判断，
与
哪一个更适宜作价格关于时间的回归方程类型？（不必说明理由）
（2）根据判断结果和表中数据，建立关于的回归方程；
（3）若该产品的日销售量
（件）与时间的函数关系为
（
），求该产品投放市场第几天的销售额最高？最高为多少元？（结果保留整数）
附：对于一组数据
，
，
，
，
，其回归直线
的斜率和截距的最小二乘估计分别为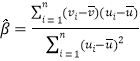
，
.
