题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)讨论![]() 极值点的个数;
极值点的个数;
(2)若![]() ,不等式
,不等式![]() 恒成立,当
恒成立,当![]() 为正数时,求
为正数时,求![]() 的最小值.
的最小值.
【答案】(1)![]() 时,
时,![]() 在
在![]() 上没有极值点.当
上没有极值点.当![]() 时,
时,![]() 在
在![]() 上有两个极值点; (2)
上有两个极值点; (2)![]() .
.
【解析】
(1)求导可得![]() ,可知导函数的最小值为
,可知导函数的最小值为![]() ,当
,当![]() 时,
时,![]() 恒成立,没有极值点,当
恒成立,没有极值点,当![]() 时,
时,![]() ,由于
,由于![]() ,只需要讨论二次方程
,只需要讨论二次方程![]() 的解得情况即可;(2)不等式
的解得情况即可;(2)不等式![]() 恒成立,即
恒成立,即![]() 恒成立,构造函数
恒成立,构造函数![]() ,对其求导,求出它的最小值为
,对其求导,求出它的最小值为![]() ,即
,即![]() ,然后结合基本不等式即可求出
,然后结合基本不等式即可求出![]() 的最小值。
的最小值。
(1)![]() ,
,
![]()
![]() 时,
时,![]() 恒成立,
恒成立,
![]() 在
在![]() 上是增函数,没有极值点.
上是增函数,没有极值点.
当![]() 时,
时,![]() ,
,
二次方程![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() 二次方程
二次方程![]() 有两个不等的正根.
有两个不等的正根.
![]() 在
在![]() 上有两个根,
上有两个根,![]() 在
在![]() 上有两个极值点.
上有两个极值点.
综上所述,![]() 时,
时,![]() 在
在![]() 上没有极值点.当
上没有极值点.当![]() 时,
时,![]() 在
在![]() 上有两个极值点.
上有两个极值点.
(2)不等式![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
记![]() ,
,
![]() ,
,
![]() 时,
时,![]() ,
,![]() ,
,![]() 在上是增函数,
在上是增函数,
![]() 时,
时,![]() ,
,![]() ,
,![]() 在上是减函数,
在上是减函数,
![]() ,
,![]()
当![]() 为正数时,
为正数时,
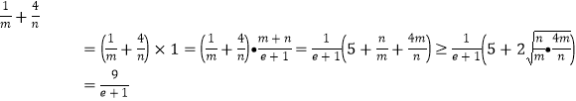 ,
,
当且仅当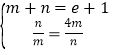 即
即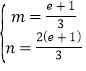 时取等号.
时取等号.
![]() 的最小值为
的最小值为![]() .
.

【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况的优惠活动评价的
条较为详细的评价信息进行统计,车辆状况的优惠活动评价的![]() 列联表如下:
列联表如下:
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对车辆状况好评 |
|
|
|
对车辆状况不满意 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过
向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过![]() 转赠给好友.某用户共获得了
转赠给好友.某用户共获得了![]() 张骑行券,其中只有
张骑行券,其中只有![]() 张是一元券.现该用户从这
张是一元券.现该用户从这![]() 张骑行券中随机选取
张骑行券中随机选取![]() 张转赠给好友,求选取的
张转赠给好友,求选取的![]() 张中至少有
张中至少有![]() 张是一元券的概率.
张是一元券的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中![]() .
.
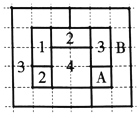
【题目】如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有![]() 升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点![]() (图2).有下列四个命题:
(图2).有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半 |
B.将容器侧面水平放置时,水面也恰好过点 |
C.任意摆放该容器,当水面静止时,水面都恰好经过点 |
D.若往容器内再注入 |
其中真命题的代号是: (写出所有真命题的代号).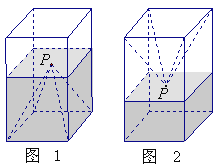
【题目】随着新高考改革的不断深入,高中学生生涯规划越来越受到社会的关注.一些高中已经开始尝试开设学生生涯规划选修课程,并取得了一定的成果.下表为某高中为了调查学生成绩与选修生涯规划课程的关系,随机抽取50名学生的统计数据.
成绩优秀 | 成绩不够优秀 | 总计 | |
选修生涯规划课 | 15 | 10 | 25 |
不选修生涯规划课 | 6 | 19 | 25 |
总计 | 21 | 29 | 50 |
(Ⅰ)根据列联表运用独立性检验的思想方法能否有![]() 的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
(Ⅱ)如果从全校选修生涯规划课的学生中随机地抽取3名学生,求抽到成绩不够优秀的学生人数![]() 的分布列和数学期望(将频率当作概率计算).
的分布列和数学期望(将频率当作概率计算).
参考附表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式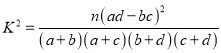 ,其中
,其中![]() .
.