题目内容
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)求证:对![]() 直线
直线![]() 与圆
与圆![]() 总有两个不同的交点;
总有两个不同的交点;
(2)是否存在实数![]() ,使得圆
,使得圆![]() 上有四个点到直线
上有四个点到直线![]() 的距离为
的距离为![]() ?若存在,求出
?若存在,求出![]() 的范围,若不存在,说明理由.
的范围,若不存在,说明理由.
【答案】(1)证明见解析;(2)存在;![]() 或
或![]() .
.
【解析】
(1)写出圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,再根据点到直线的距离公式,求出圆心到直线
,再根据点到直线的距离公式,求出圆心到直线![]() 的距离
的距离![]() ,结合题意判断得出
,结合题意判断得出![]() ,即可证明:对
,即可证明:对![]() ,直线
,直线![]() 与圆
与圆![]() 总有两个不同的交点;
总有两个不同的交点;
(2)要使得圆![]() 上有四个点到直线
上有四个点到直线![]() 的距离为
的距离为![]() ,则要求圆心
,则要求圆心![]() 到直线
到直线![]() 的距离小于
的距离小于![]() ,解不等式即可求出
,解不等式即可求出![]() 的范围.
的范围.
解:(1)证明:圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,
,
所以圆心![]() 到直线
到直线![]() 的距离为:
的距离为:
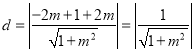 ,
,
由于![]() ,则
,则![]() ,即
,即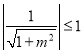 ,
,
则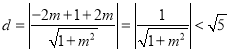 ,
,
所以直线![]() 与圆
与圆![]() 相交,即直线
相交,即直线![]() 与圆
与圆![]() 总有两个不同的交点.
总有两个不同的交点.
(2)假设存在直线![]() ,使得圆上有四点到直线
,使得圆上有四点到直线![]() 的距离为
的距离为![]() ,
,
由于圆心![]() ,半径为
,半径为![]() ,
,
则圆心![]() 到直线
到直线![]() 的距离小于
的距离小于![]() ,
,
则圆心![]() 到直线
到直线![]() 的距离为:
的距离为:
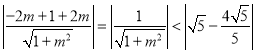 ,
,
化简得![]() ,
,
解得:![]() 或
或![]() .
.

练习册系列答案
相关题目
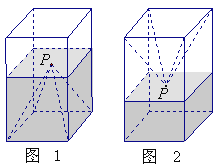
【题目】如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有![]() 升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点![]() (图2).有下列四个命题:
(图2).有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半 |
B.将容器侧面水平放置时,水面也恰好过点 |
C.任意摆放该容器,当水面静止时,水面都恰好经过点 |
D.若往容器内再注入 |
其中真命题的代号是: (写出所有真命题的代号).