题目内容
【题目】已知函数f(x)=|2x﹣a|+|x﹣a+1|.
(1)当a=4时,求解不等式f(x)≥8;
(2)已知关于x的不等式f(x)![]() 在R上恒成立,求参数a的取值范围.
在R上恒成立,求参数a的取值范围.
【答案】(1)[5,+∞)∪(∞,![]() ];(2)[﹣2,1].
];(2)[﹣2,1].
【解析】
(1)根据a=4时,有f(x)=|2x﹣4|+|x﹣3|,然后利用绝对值的几何意义,去绝对值求解.
(2)根据绝对值的零点有a﹣1和![]() ,分a﹣1
,分a﹣1![]() ,a﹣1
,a﹣1![]() 和a﹣1
和a﹣1![]() 时三种情况分类讨论求解.
时三种情况分类讨论求解.
(1)当a=4时,f(x)=|2x﹣4|+|x﹣3|,
(i)当x≥3时,原不等式可化为3x﹣7≥8,解可得x≥5,
此时不等式的解集[5,+∞);
(ii)当2<x<3时,原不等式可化为2x﹣4+3﹣x≥8,解可得x≥9
此时不等式的解集;
(iii)当x≤2时,原不等式可化为﹣3x+7≥8,解可得x![]() ,
,
此时不等式的解集(∞,![]() ],
],
综上可得,不等式的解集[5,+∞)∪(∞,![]() ],
],
(2)(i)当a﹣1![]() 即a=2时,f(x)=3|x﹣1|
即a=2时,f(x)=3|x﹣1|![]() 2显然不恒成立,
2显然不恒成立,
(ii)当a﹣1![]() 即a>2时,
即a>2时,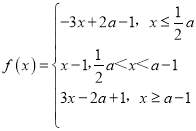 ,
,
结合函数的单调性可知,当x![]() 时,函数取得最小值f(
时,函数取得最小值f(![]() )
)![]() ,
,
若f(x)![]() 在R上恒成立,则
在R上恒成立,则![]() ,此时a不存在,
,此时a不存在,
(iii)当a﹣1![]() 即a<2时,f(x)
即a<2时,f(x)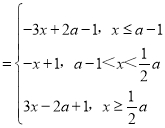
若f(x)![]() 在R上恒成立,则1
在R上恒成立,则1![]() ,
,
解得﹣2≤a≤1,
此时a的范围[﹣2,1],
综上可得,a的范围围[﹣2,1].

【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查.现在按课外阅读时间的情况将学生分成三类:![]() 类(不参加课外阅读),
类(不参加课外阅读),![]() 类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),
类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),![]() 类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时).调查结果如下表:
类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时).调查结果如下表:
|
|
| |
男生 |
| 5 | 3 |
女生 |
| 3 | 3 |
(1)求出表中![]() ,
,![]() 的值;
的值;
(2)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | ||
不参加课外阅读 | ||||
参加课外阅读 | ||||
总计 |
P(K≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |