题目内容
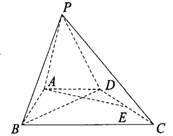
【题目】已知四棱锥
的底面
是直角梯形，
，
，
为
的中点，
.
（1）证明:平面
平面；
（2）若
与平面所成的角为
，求二面角
的余弦值.
【答案】（1）见解析；（2）
【解析】分析：（1）在直角梯形
中，由已知得
是等边三角形，这样结合
可得
，再有
，因此有
平面
，从而可证面面垂直；
（2）只要作
于点
，则可得
平面，从而得是
中点，
，计算得
，以
为坐标轴建立空间直角坐标系，写出各点坐标，求出平面
和平面
的法向量，由法向量的夹角的余弦值得二面角的余弦值．
详解：（1）证明：由是直角梯形，
，
可得
从而
是等边三角形，
，平分
∵
为
的中点，
，∴
又∵
，∴平面
∵
平面，∴平面
平面
（2）法一：作于,连
,
∵平面平面,平面
平面
∴与平面平面
∴
为
与平面所成的角，，
又∵
,∴为中点,
以为
轴建立空间直角坐标系，
，
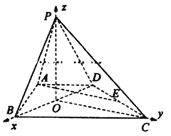
设平面
的一个法向量
，
由
得
，
令
得
，
又平面的一个法向量为
，
设二面角
为
，则
所求二面角的余弦值是.
解法二：作于点,连，
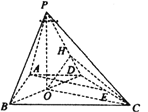
∵平面平面，平面平面
∴
平面
∴为与平面所成的角,
又∵,∴为中点，
作
于点
,连
,则
平面
，则
，
则
为所求二面角的平面角
由
，得
,∴
,∴
.
【题目】根据我市房地产数据显示，今年我市前5个月新建住宅销售均价逐月上升，为抑制房价过快上涨，政府从6月份开始推出限价房等宏观调控措施，6月份开始房价得到很好的抑制，房价回落．今年前10个月的房价均价如表：
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
均价y（万元/平方米） | 0.83 | 0.95 | 1.00 | 1.05 | 1.17 | 1.15 | 1.10 | 1.06 | 0.98 | 0.94 |
地产数据研究发现，从1月份至5月份的各月均价y（万元/平方米）与x之间具有正线性相关关系，从6月份至10月份的各月均价y（万元/平方米）与x之间具有负线性相关关系．
（1）若政府不调控，根据前5个月的数据，求y关于x的回归直线方程，并预测12月份的房地产均价．（精确到0.01）
（2）政府调控后，从6月份至10月份的数据可得到y与x的回归直线方程为：
．由此预测政府调控后12月份的房地产均价．说明政府调控的必要性．（精确到0.01）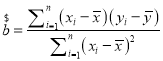
；
；
【题目】2019年12月16日，公安部联合阿里巴巴推出的“钱盾反诈机器人”正式上线，当普通民众接到电信网络诈骗电话，公安部钱盾反诈预警系统预警到这一信息后，钱盾反诈机器人即自动拨打潜在受害人的电话予以提醒，来电信息显示为“公安反诈专号”.某法制自媒体通过自媒体调查民众对这一信息的了解程度，从5000多参与调查者中随机抽取200个样本进行统计，得到如下数据：男性不了解这一信息的有50人，了解这一信息的有80人，女性了解这一信息的有40人.
（1）完成下列
列联表，问：能否在犯错误的概率不超过0.01的前提下，认为200个参与调查者是否了解这一信息与性别有关？
了解 | 不了解 | 合计 | |
男性 | |||
女性 | |||
合计 |
（2）该自媒体对200个样本中了解这一信息的调查者按照性别分组，用分层抽样的方法抽取6人，再从这6人中随机抽取3人给予一等奖，另外3人给予二等奖，求一等奖与二等奖获得者都有女性的概率.
附：
P(K2≥k) | 0.01 | 0.005 | 0.001 |
k | 6.635 | 7.879 | 10.828 |
