题目内容
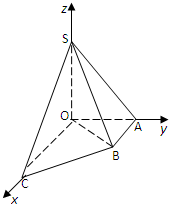
如图直角梯形OABC中,∠COA=∠AOB=90°,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,分别以OC,OA,OS为x轴、y轴、z轴建立直角坐标系O-xyz.
(Ⅰ)求
与
夹角的余弦值;
(Ⅱ)求OC与平面SBC夹角的正弦值;
(Ⅲ)求二面角S-BC-O.
(Ⅰ)求
| SC |
| OB |
(Ⅱ)求OC与平面SBC夹角的正弦值;
(Ⅲ)求二面角S-BC-O.

(Ⅰ)如图所示:C(2,0,0),S(0,0,1),O(0,0,0),B(1,1,0).
∴
=(2,0,-1),
=(1,1,0),
∴cos<
,
>=
=
.
∴
与
夹角的余弦值为
.…(3分)
(Ⅱ)设平面SBC的法向量
=(1,p,q),
∵
=(2,0,-1),
=(-1,1,0),
∴
,∴
,
∴
=(1,1,2),…(6分)
又∵
=(2,0,0),
∴cos<
,
>=
=
=
∴OC与平面SBC夹角的正弦值为
;…(8分)
(Ⅲ)∵SO⊥平面OABC,∴
=(0,0,1)为平面OABC的法向量.
又∵平面SBC的法向量
=(1,1,2),
∴cos<
,
>=
=
=
.
∴二面角S-BC-O的余弦值为
.…(12分)

∴
| SC |
| OB |
∴cos<
| SC |
| OB |
| 2 | ||||
|
| ||
| 5 |
∴
| SC |
| OB |
| ||
| 5 |
(Ⅱ)设平面SBC的法向量
| n |
∵
| SC |
| CB |
∴
|
|
∴
| n |
又∵
| OC |
∴cos<
| n |
| OC |
| ||||
|
|
| 2 | ||
|
| ||
| 6 |
∴OC与平面SBC夹角的正弦值为
| ||
| 6 |
(Ⅲ)∵SO⊥平面OABC,∴
| OS |
又∵平面SBC的法向量
| n |
∴cos<
| n |
| OS |
| ||||
|
|
| 2 | ||
|
| ||
| 3 |
∴二面角S-BC-O的余弦值为
| ||
| 3 |


练习册系列答案
相关题目


 =a,
=a, =b,
=b,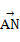 =3
=3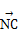 ,M为BC的中点,则
,M为BC的中点,则 =______(用a,b表示).
=______(用a,b表示).