题目内容
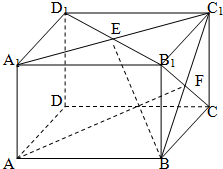
如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点.
(Ⅰ)求证:A1B∥平面ADC1;
(Ⅱ)求二面角C1-AD-C的余弦值;
(Ⅲ)试问线段A1B1上是否存在点E,使AE与DC1成60°角?若存在,确定E点位置,若不存在,说明理由.
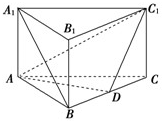
(Ⅰ)求证:A1B∥平面ADC1;
(Ⅱ)求二面角C1-AD-C的余弦值;
(Ⅲ)试问线段A1B1上是否存在点E,使AE与DC1成60°角?若存在,确定E点位置,若不存在,说明理由.

(Ⅰ)证明:连接A1C,交AC1于点O,连接OD.
由ABC-A1B1C1是直三棱柱,得四边形ACC1A1为矩形,O为A1C的中点.
又D为BC中点,所以OD为△A1BC中位线,
所以A1B∥OD,
因为OD?平面ADC1,A1B?平面ADC1,
所以A1B∥平面ADC1.…(4分)
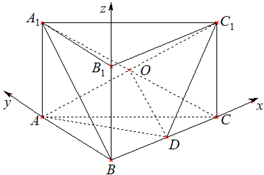
(Ⅱ)由ABC-A1B1C1是直三棱柱,且∠ABC=90°,
故BA,BC,BB1两两垂直.
如图建立空间直角坐标系B-xyz.设BA=2,则B(0,0,0),C(2,0,0),A(0,2,0),C1(2,0,1),D(1,0,0).
所以
=(1,-2,0),
=(2,-2,1)
设平面ADC1的法向量为
=(x,y,z),则有
所以
取y=1,得
=(2,1,-2).
平面ADC的法向量为
=(0,0,1).
由二面角C1-AD-C是锐角,得cos<
,
>=
=
.…(8分)
所以二面角C1-AD-C的余弦值为
.
(Ⅲ)假设存在满足条件的点E.
因为E在线段A1B1上,A1(0,2,1),B1(0,0,1),故可设E(0,λ,1),其中0≤λ≤2.
所以
=(0,λ-2,1),
=(1,0,1).
因为AE与DC1成60°角,所以|
|=
.
即|
|=
,解得λ=1,舍去λ=3.
所以当点E为线段A1B1中点时,AE与DC1成60°角.…(12分)
由ABC-A1B1C1是直三棱柱,得四边形ACC1A1为矩形,O为A1C的中点.
又D为BC中点,所以OD为△A1BC中位线,
所以A1B∥OD,
因为OD?平面ADC1,A1B?平面ADC1,
所以A1B∥平面ADC1.…(4分)
(Ⅱ)由ABC-A1B1C1是直三棱柱,且∠ABC=90°,
故BA,BC,BB1两两垂直.
如图建立空间直角坐标系B-xyz.设BA=2,则B(0,0,0),C(2,0,0),A(0,2,0),C1(2,0,1),D(1,0,0).
所以
| AD |
| AC1 |
设平面ADC1的法向量为
| n |
|
所以
|
| n |
平面ADC的法向量为
| v |
由二面角C1-AD-C是锐角,得cos<
| n |
| v |
|
| ||||
|
|
| 2 |
| 3 |
所以二面角C1-AD-C的余弦值为
| 2 |
| 3 |
(Ⅲ)假设存在满足条件的点E.
因为E在线段A1B1上,A1(0,2,1),B1(0,0,1),故可设E(0,λ,1),其中0≤λ≤2.
所以
| AE |
| DC1 |
因为AE与DC1成60°角,所以|
| ||||
|
|
| 1 |
| 2 |
即|
| 1 | ||||
|
| 1 |
| 2 |
所以当点E为线段A1B1中点时,AE与DC1成60°角.…(12分)


练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 是直角边等于4的等腰直角三角形,
是直角边等于4的等腰直角三角形,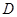 是斜边
是斜边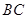 的中点,
的中点,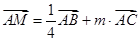 ,向量
,向量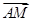 的终点
的终点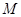 在
在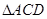 的内部(不含边界),则实数
的内部(不含边界),则实数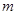 的取值范围是 .
的取值范围是 .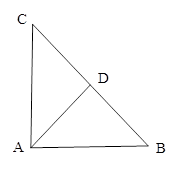
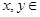 R,向量
R,向量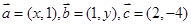 且
且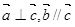 ,则
,则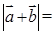 ( )
( )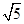
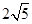
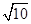
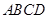 为平行四边形,若向量
为平行四边形,若向量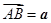 ,
,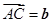 ,则向量
,则向量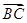 为( )
为( )