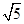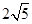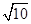题目内容
如图(1),等腰直角三角形ABC的底边AB=4,点D在线段AC上,DE⊥AB于E,现将△ADE沿DE折起到△PDE的位置(如图(2)).
(Ⅰ)求证:PB⊥DE;
(Ⅱ)若PE⊥BE,直线PD与平面PBC所成的角为30°,求PE长.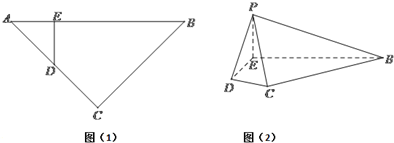
(Ⅰ)求证:PB⊥DE;
(Ⅱ)若PE⊥BE,直线PD与平面PBC所成的角为30°,求PE长.

(Ⅰ)∵DE⊥AB,∴DE⊥BE,DE⊥PE,….(2分)
∵BE∩PE=E,∴DE⊥平面PEB,
又∵PB?平面PEB,∴BP⊥DE;….(4分)
(Ⅱ)∵PE⊥BE,PE⊥DE,DE⊥BE,
∴分别以DE、BE、PE所在直线为x轴、y轴、z轴建立空间直角坐标系(如图),…(5分)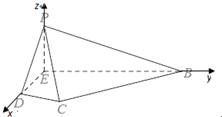
设PE=a,则B(0,4-a,0),D(a,0,0),C(2,2-a,0),
P(0,0,a),…(7分)
可得
=(0,4-a,-a),
=(2,-2,0),…(8分)
设面PBC的法向量
=(x,y,z),
∴
令y=1,可得x=1,z=
因此
=(1,1,
)是面PBC的一个法向量,…(10分)
∵
=(a,0,-a),PD与平面PBC所成角为30°,…(12分)
∴sin30°=|cos<
,
>|,即|
|=
,…(11分)
解之得:a=
,或a=4(舍),因此可得PE的长为
.…(13分)
∵BE∩PE=E,∴DE⊥平面PEB,
又∵PB?平面PEB,∴BP⊥DE;….(4分)
(Ⅱ)∵PE⊥BE,PE⊥DE,DE⊥BE,
∴分别以DE、BE、PE所在直线为x轴、y轴、z轴建立空间直角坐标系(如图),…(5分)

设PE=a,则B(0,4-a,0),D(a,0,0),C(2,2-a,0),
P(0,0,a),…(7分)
可得
| PB |
| BC |
设面PBC的法向量
| n |
∴
|
| 4-a |
| a |
因此
| n |
| 4-a |
| a |
∵
| PD |
∴sin30°=|cos<
| PD |
| n |
| a-(4-a) | ||||||
|
| 1 |
| 2 |
解之得:a=
| 4 |
| 5 |
| 4 |
| 5 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
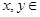 R,向量
R,向量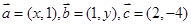 且
且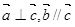 ,则
,则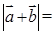 ( )
( )