题目内容
如图,四棱锥P-ABCD的底面是平行四边形,PA⊥平面ABCD,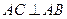 ,
,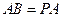 ,点E是PD上的点,且DE=
,点E是PD上的点,且DE=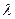 PE(0<
PE(0<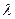
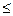 1).
1).
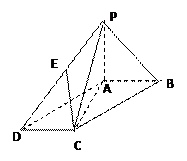
(Ⅰ) 求证:PB⊥AC;
(Ⅱ) 求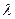 的值,使
的值,使 平面ACE;
平面ACE;
(Ⅲ) 当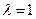 时,求二面角E-AC-B的大小.
时,求二面角E-AC-B的大小.
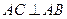 ,
,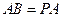 ,点E是PD上的点,且DE=
,点E是PD上的点,且DE=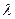 PE(0<
PE(0<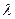
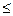 1).
1). 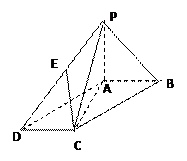
(Ⅰ) 求证:PB⊥AC;
(Ⅱ) 求
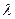 的值,使
的值,使 平面ACE;
平面ACE;(Ⅲ) 当
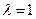 时,求二面角E-AC-B的大小.
时,求二面角E-AC-B的大小.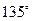
解:(Ⅰ)证明: 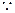 PA
PA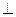 平面ABCD,
平面ABCD,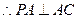
又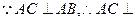 平面PAB,
平面PAB,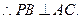
(Ⅱ)解:连结BD交AC于O,连结OE,
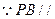 平面ACE,平面AEC
平面ACE,平面AEC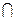 平面PBD
平面PBD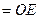
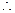
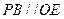 ,又
,又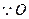 为平行四边形ABCD的对角线BD的中点
为平行四边形ABCD的对角线BD的中点
 E为PD的中点,故
E为PD的中点,故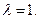
(Ⅲ)取AD的中F,连结,EF,则
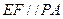
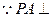 平面ABCD,
平面ABCD,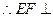 平面ABCD
平面ABCD
连结OF,则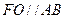
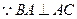 ,
,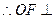 AC,
AC,
连结EF,则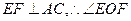 就是求二面角
就是求二面角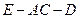 的平面角,
的平面角,
又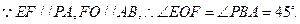
 二面角
二面角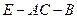 大小为
大小为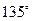
 PA
PA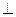 平面ABCD,
平面ABCD,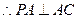
又
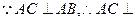 平面PAB,
平面PAB,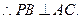
(Ⅱ)解:连结BD交AC于O,连结OE,
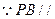 平面ACE,平面AEC
平面ACE,平面AEC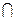 平面PBD
平面PBD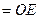
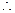
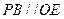 ,又
,又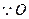 为平行四边形ABCD的对角线BD的中点
为平行四边形ABCD的对角线BD的中点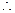 E为PD的中点,故
E为PD的中点,故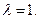
(Ⅲ)取AD的中F,连结,EF,则
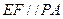
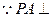 平面ABCD,
平面ABCD,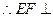 平面ABCD
平面ABCD连结OF,则
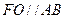
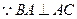 ,
,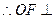 AC,
AC,连结EF,则
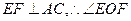 就是求二面角
就是求二面角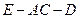 的平面角,
的平面角,又
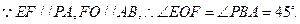
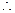 二面角
二面角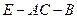 大小为
大小为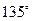

练习册系列答案
相关题目
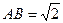 ,
,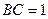 ,现沿对角线
,现沿对角线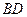 折成二面角
折成二面角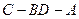 ,使
,使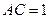 (如图).
(如图).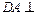 面
面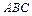 ;
;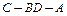 平面角的大小.
平面角的大小.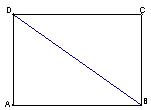

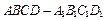 中,点
中,点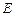 在棱
在棱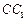 的延长线上,且
的延长线上,且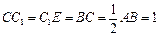 .下标
.下标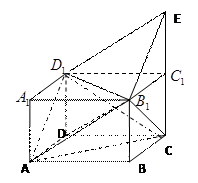
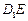 ∥平面
∥平面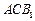 ;
;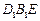
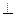 平面
平面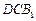 ;
;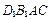 的体积.
的体积.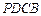 中,
中,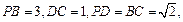
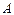 为
为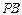 边上一点,
边上一点,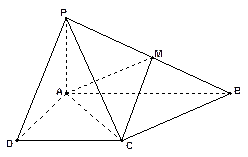
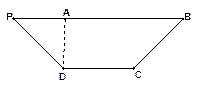
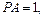 将
将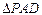 沿
沿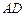 折起,使平面
折起,使平面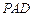 ⊥平面
⊥平面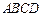 .
.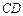 ⊥平面
⊥平面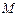 是侧棱
是侧棱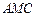 把几何体分成的两部分的体积之比。
把几何体分成的两部分的体积之比。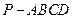 的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.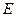 是侧棱
是侧棱 上的动点.
上的动点.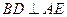
 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.
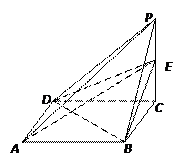
 的顶点
的顶点 ,
,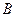 ,
,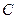 分别在两两垂直的三条射线
分别在两两垂直的三条射线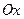 ,
,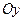 ,
, 上,则在下列命题中,正确命题的个数为_______.
上,则在下列命题中,正确命题的个数为_______.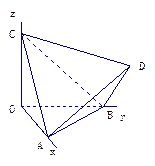
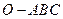 是正三棱锥 ;
是正三棱锥 ; ∥平面
∥平面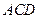 ;
;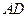 与
与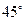 ;
;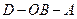 为
为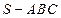 中,底面
中,底面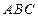 为边长等于2的等边三角形,
为边长等于2的等边三角形,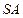 垂直于底面
垂直于底面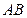 与平面
与平面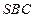 所成角的正弦值为
所成角的正弦值为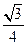
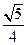
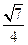
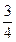
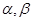 是不同的两个平面,直线
是不同的两个平面,直线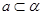 ,直线
,直线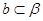 ,条件
,条件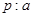 与
与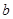 没有公共点,条件
没有公共点,条件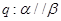 ,则
,则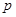 是
是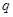 的
的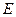 在棱
在棱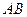 上,
上,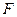 在棱
在棱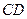 上.并且
上.并且 (0<l<+∞),设a为异面直线
(0<l<+∞),设a为异面直线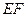 与
与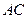 所成的角,b 为异面直线EF与BD所成的角,则a+b的值是
所成的角,b 为异面直线EF与BD所成的角,则a+b的值是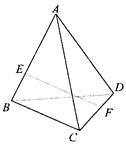
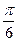
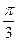
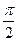
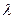 的值有关
的值有关