题目内容
如图,正三棱锥A-BCD中,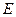 在棱
在棱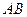 上,
上,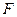 在棱
在棱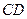 上.并且
上.并且 (0<l<+∞),设a为异面直线
(0<l<+∞),设a为异面直线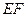 与
与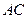 所成的角,b 为异面直线EF与BD所成的角,则a+b的值是
所成的角,b 为异面直线EF与BD所成的角,则a+b的值是
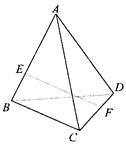
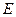 在棱
在棱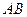 上,
上,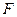 在棱
在棱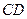 上.并且
上.并且 (0<l<+∞),设a为异面直线
(0<l<+∞),设a为异面直线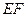 与
与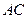 所成的角,b 为异面直线EF与BD所成的角,则a+b的值是
所成的角,b 为异面直线EF与BD所成的角,则a+b的值是
A.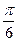 | B.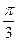 | C.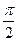 | D.与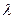 的值有关 的值有关 |
C
略

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
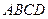 为平行四边形,
为平行四边形, ,
,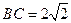 ,
,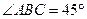 ,
, 是长方形,
是长方形,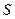 是
是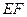 的中点,
的中点,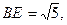 平面
平面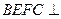 平面
平面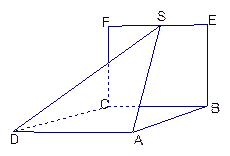
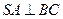 ;
;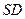 与平面
与平面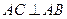 ,
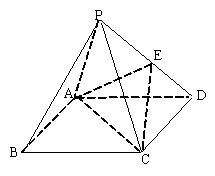
,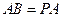 ,点E是PD上的点,且DE=
,点E是PD上的点,且DE=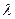 PE(0<
PE(0<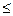 1).
1). 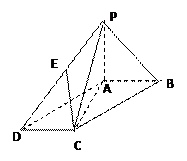
 平面ACE;
平面ACE; 时,求二面角E-AC-B的大小.
时,求二面角E-AC-B的大小. 1D1中,底面ABCD是梯形BC∥AD,∠DAB=90°,AB=BB1=4,BC=3,AD=5,AE=3,F、G分别为CD、C1D1的中点.
1D1中,底面ABCD是梯形BC∥AD,∠DAB=90°,AB=BB1=4,BC=3,AD=5,AE=3,F、G分别为CD、C1D1的中点.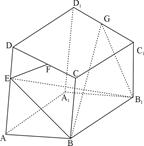
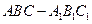 的底面是直角三角形,
的底面是直角三角形,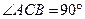 ,点
,点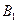 在底面
在底面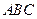 上的射影恰好是
上的射影恰好是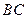 的中点,且
的中点,且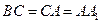 .
.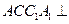 平面
平面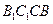 ;
;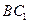
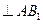 ;
;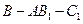 的大小.
的大小. 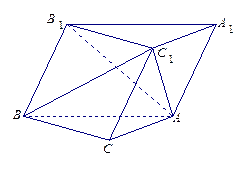
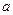 、
、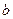 、
、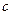 是直线,
是直线,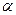 是平面,给出下列命题:①若
是平面,给出下列命题:①若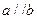 ,
,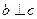 ,则
,则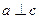 ;
;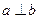 ,
,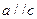 ;③若
;③若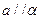 ,
,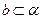 ,则
,则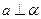 ,
,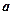 、
、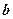 是两条异面直线,
是两条异面直线,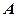 是
是