题目内容
(本小题满分12分)已知矩形ABCD中,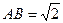 ,
,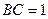 ,现沿对角线
,现沿对角线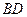 折成二面角
折成二面角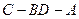 ,使
,使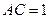 (如图).
(如图).
(I)求证: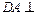 面
面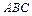 ;
;
(II)求二面角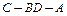 平面角的大小.
平面角的大小.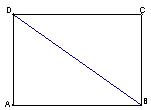

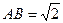 ,
,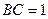 ,现沿对角线
,现沿对角线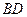 折成二面角
折成二面角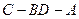 ,使
,使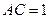 (如图).
(如图).(I)求证:
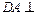 面
面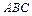 ;
;(II)求二面角
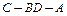 平面角的大小.
平面角的大小.

(I)证明见解析
(II)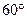
(II)
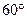
(I)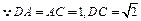 ,
,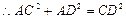 ,
,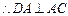 . …3分
. …3分
又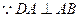 ,
,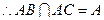
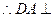 平面
平面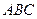 . 6分
. 6分
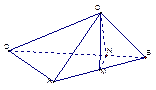
(II)方法一:取AB中点M,连CM,过M作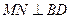 交BD于N,连CN.
交BD于N,连CN.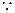
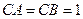 ,
,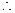
 ,
,
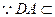 平面
平面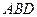 ,
,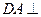 平面
平面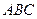 ,
, 平面
平面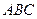
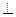 平面
平面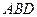 . ………8分
. ………8分
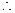
 平面
平面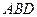 ,
,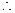

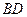 .又
.又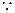
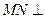
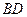 ,
,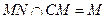
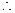
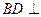 平面
平面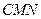 ,
,
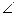
 为二面角
为二面角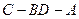 的平
的平 面角.…10分
面角.…10分
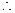
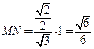 ,
,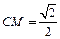 ,
,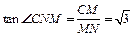 ,
, ,
,
故二面角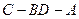 平面角的度数为
平面角的度数为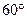 . …………12分
. …………12分
方法二:取AB中点M,连CM.∵AC=AB=1, ∴CM⊥AB.
又∵平面ABC⊥平面ABD,∴CM⊥平面ABD. 取BD中点H,∴MH∥AD.
∵AD⊥AB, ∴MH⊥AB.
分别以AB,MH,MC为x,y,z轴建立空间直角坐标系. …………6分
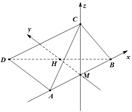
得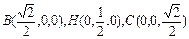 ,
,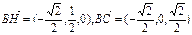 . 8分
. 8分
设平面BCD的法向量为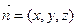 ,
,
∴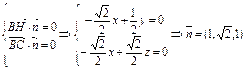 . 10分
. 10分
又∵平面ABD的法向量为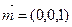 ,
,
∴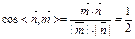 显然二面角
显然二面角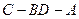 为锐角,所以它的大小为
为锐角,所以它的大小为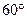 .12分
.12分
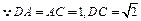 ,
,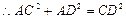 ,
,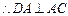 . …3分
. …3分又
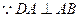 ,
,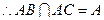
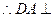 平面
平面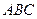 . 6分
. 6分
(II)方法一:取AB中点M,连CM,过M作
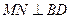 交BD于N,连CN.
交BD于N,连CN.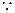
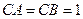 ,
,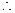
 ,
,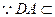 平面
平面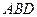 ,
,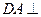 平面
平面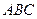 ,
, 平面
平面
 平面
平面 . ………8分
. ………8分
 平面
平面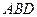 ,
,

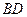 .又
.又
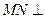
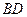 ,
,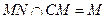
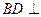 平面
平面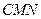 ,
,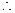
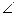
 为二面角
为二面角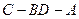 的平
的平 面角.…10分
面角.…10分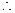
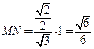 ,
,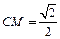 ,
,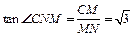 ,
, ,
,故二面角
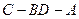 平面角的度数为
平面角的度数为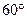 . …………12分
. …………12分方法二:取AB中点M,连CM.∵AC=AB=1, ∴CM⊥AB.
又∵平面ABC⊥平面ABD,∴CM⊥平面ABD. 取BD中点H,∴MH∥AD.
∵AD⊥AB, ∴MH⊥AB.
分别以AB,MH,MC为x,y,z轴建立空间直角坐标系. …………6分

得
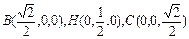 ,
,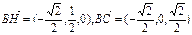 . 8分
. 8分设平面BCD的法向量为
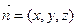 ,
,∴
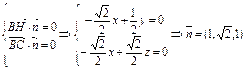 . 10分
. 10分又∵平面ABD的法向量为
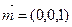 ,
, ∴
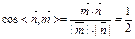 显然二面角
显然二面角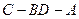 为锐角,所以它的大小为
为锐角,所以它的大小为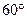 .12分
.12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
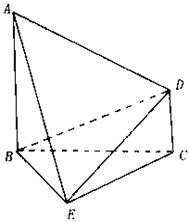
 中,
中,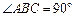 ,
,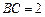 ,
,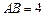 ,
,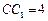 ,E在
,E在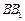 上,且
上,且 ,
,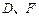 分别为
分别为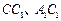 的中点.
的中点.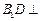 平面
平面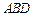 ;
;  与
与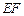 所成的角;
所成的角;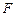 到平面
到平面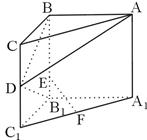
 B
B 平面ABCD,底面ABCD是边长为1的正方形,侧棱AA
平面ABCD,底面ABCD是边长为1的正方形,侧棱AA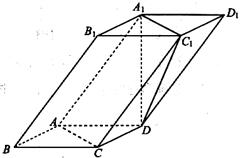
 平面
平面 是正三角形,
是正三角形, 。
。
 与
与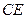 所成角的余弦值;
所成角的余弦值;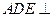 平面
平面 ;
; 的余弦值。
的余弦值。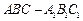 中,侧面
中,侧面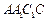
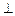 底面
底面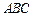 ,
,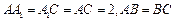 ,
, ,O为
,O为 中点.
中点.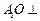 平面
平面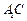 与平面
与平面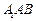 所成角的正弦值;
所成角的正弦值;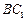 上是否存在一点
上是否存在一点 ,使得
,使得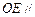 平面
平面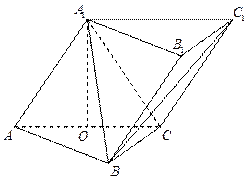
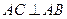 ,
,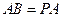 ,点E是PD上的点,且DE=
,点E是PD上的点,且DE=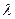 PE(0<
PE(0<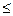 1).
1). 
 平面ACE;
平面ACE; 时,求二面角E-AC-B的大小.
时,求二面角E-AC-B的大小. 1D1中,底面ABCD是梯形BC∥AD,∠DAB=90°,AB=BB1=4,BC=3,AD=5,AE=3,F、G分别为CD、C1D1的中点.
1D1中,底面ABCD是梯形BC∥AD,∠DAB=90°,AB=BB1=4,BC=3,AD=5,AE=3,F、G分别为CD、C1D1的中点.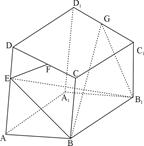
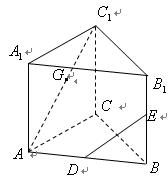
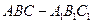 中,
中,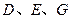 分别是
分别是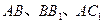 的中点,
的中点,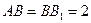 .
.
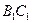 上是否存在点
上是否存在点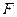 使
使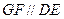 ?如果存在,试确定它的位置;如果不存在,请说明理由;
?如果存在,试确定它的位置;如果不存在,请说明理由;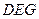 与底面
与底面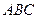 所成锐二面角的正切值;
所成锐二面角的正切值;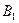 到截面
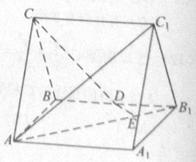
到截面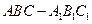 中,
中,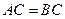 ,
,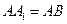 ,
,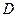 为
为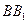 的中点,
的中点,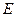 为
为 上的一点,
上的一点,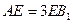 .
.
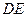 为异面直线
为异面直线 的公垂线;
的公垂线;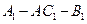 的大小.
的大小.