题目内容
二次函数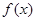 满足
满足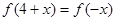 ,且
,且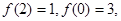 若
若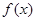 在
在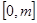 上有最小值1,最大值3,则实数
上有最小值1,最大值3,则实数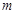 的取值范围是
的取值范围是
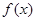 满足
满足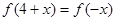 ,且
,且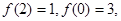 若
若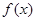 在
在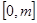 上有最小值1,最大值3,则实数
上有最小值1,最大值3,则实数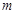 的取值范围是
的取值范围是A.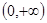 | B.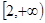 | C.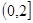 | D.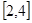 |
D
∵二次函数f(x)满足f(4+x)=f(-x),
∴函数的对称轴为直线x=2,故可设函数解析式为f(x)=a(x-2)2+h,
∵f(2)=1,f(0)=3,
∴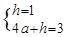 ,解得
,解得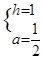 ∴f(x)=
∴f(x)=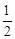 (x-2)2+1
(x-2)2+1
令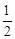 (x-2)2+1=3,则x=0或x=4
(x-2)2+1=3,则x=0或x=4
∵f(x)在[0,m]上有最小值1,最大值3,
∴实数m的取值范围是[2,4].
故选D.
∴函数的对称轴为直线x=2,故可设函数解析式为f(x)=a(x-2)2+h,
∵f(2)=1,f(0)=3,
∴
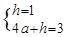 ,解得
,解得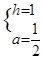 ∴f(x)=
∴f(x)=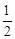 (x-2)2+1
(x-2)2+1令
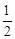 (x-2)2+1=3,则x=0或x=4
(x-2)2+1=3,则x=0或x=4∵f(x)在[0,m]上有最小值1,最大值3,
∴实数m的取值范围是[2,4].
故选D.

练习册系列答案
相关题目
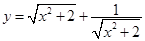 ②
② 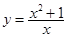
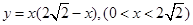 ④
④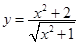
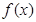 在区间D上的最大值与最小值分别为
在区间D上的最大值与最小值分别为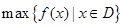 与
与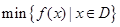 .设函数
.设函数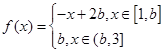 ,
,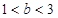 .
.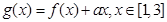 .
.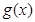 在
在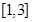 上单调递减,求
上单调递减,求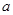 的取值范围;
的取值范围;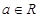 .令
.令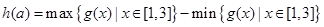 .
.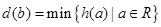 .试写出
.试写出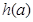 的表达式,并求
的表达式,并求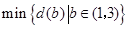 ;
;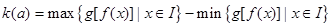 (其中I为
(其中I为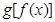 的定义域).若I恰好为
的定义域).若I恰好为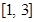 ,求b的取值范围,并求
,求b的取值范围,并求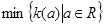 .
.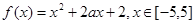
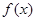 的最小值;
的最小值;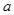 的取值范围,使
的取值范围,使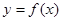 在区间
在区间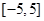 上是单调函数.
上是单调函数.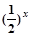
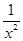 .
.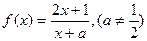 ,
,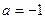 ,证明
,证明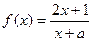 在区间
在区间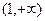 上是增函数;
上是增函数;
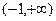 上是单调函数,试求实数
上是单调函数,试求实数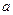 的取值范围。
的取值范围。 是(-∞,+∞)上的减函数,那么a的取值范围是
是(-∞,+∞)上的减函数,那么a的取值范围是 )
)  ,
,