题目内容
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,
第3小题满分8分.
记函数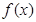 在区间D上的最大值与最小值分别为
在区间D上的最大值与最小值分别为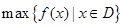 与
与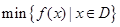 .设函数
.设函数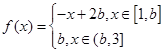 ,
,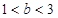 .
.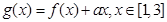 .
.
(1)若函数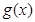 在
在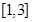 上单调递减,求
上单调递减,求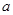 的取值范围;
的取值范围;
(2)若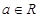 .令
.令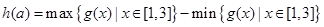 .
.
记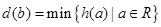 .试写出
.试写出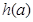 的表达式,并求
的表达式,并求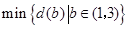 ;
;
(3)令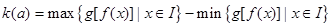 (其中I为
(其中I为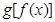 的定义域).若I恰好为
的定义域).若I恰好为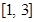 ,求b的取值范围,并求
,求b的取值范围,并求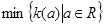 .
.
第3小题满分8分.
记函数
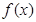 在区间D上的最大值与最小值分别为
在区间D上的最大值与最小值分别为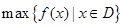 与
与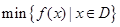 .设函数
.设函数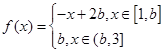 ,
,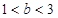 .
.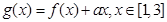 .
.(1)若函数
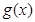 在
在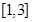 上单调递减,求
上单调递减,求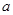 的取值范围;
的取值范围;(2)若
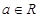 .令
.令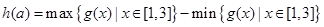 .
.记
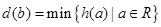 .试写出
.试写出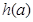 的表达式,并求
的表达式,并求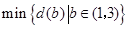 ;
;(3)令
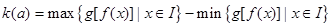 (其中I为
(其中I为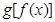 的定义域).若I恰好为
的定义域).若I恰好为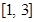 ,求b的取值范围,并求
,求b的取值范围,并求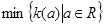 .
.解:(1)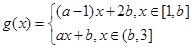 ,(2分)由题意
,(2分)由题意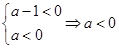 (4分)
(4分)
(2)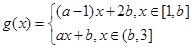
1)当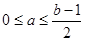 时,
时,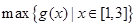 = g(1)=a+2b-1,
= g(1)=a+2b-1,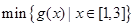 = g(b)=ab+b, 此时,
= g(b)=ab+b, 此时,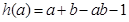
2) 当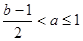 时,
时,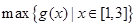 =g(3)=3a+b,
=g(3)=3a+b,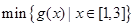 = g(b)=ab+b, 此时,
= g(b)=ab+b, 此时,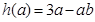
故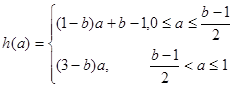 , (2分)
, (2分)
因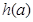 在
在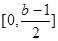 上单调递减,在
上单调递减,在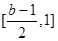 单调递增,故
单调递增,故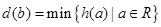 =h(
=h(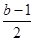 )=
)=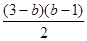 , (4分)
, (4分)
故当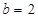 时,得
时,得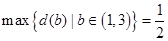 . (6分)
. (6分)
(3)ⅰ)当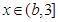 时,f(x)="b,"
时,f(x)="b," 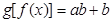
ⅱ)当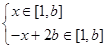 ,即
,即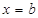 时,
时,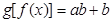
ⅲ)当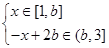 时,即
时,即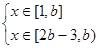 (*),(3分)
(*),(3分)
①若2b-3>1即b>2, 由(*)知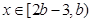 ,但此时
,但此时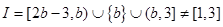 ,所以b>2不合题意。
,所以b>2不合题意。
②若2b-3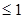 即b
即b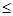 2, 由(*)知
2, 由(*)知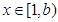 , 此时
, 此时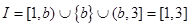
故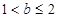 , (5分) 且
, (5分) 且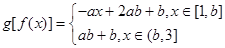
于是,当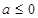 时,
时,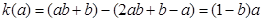
当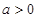 时,
时,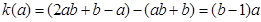
即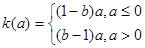 (7分)
(7分)
从而可得当a=0时, ="0. " (8分)
="0. " (8分)
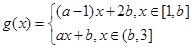 ,(2分)由题意
,(2分)由题意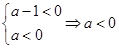 (4分)
(4分)(2)
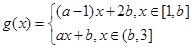
1)当
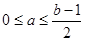 时,
时,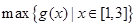 = g(1)=a+2b-1,
= g(1)=a+2b-1,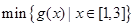 = g(b)=ab+b, 此时,
= g(b)=ab+b, 此时,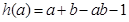
2) 当
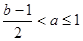 时,
时,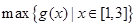 =g(3)=3a+b,
=g(3)=3a+b,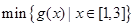 = g(b)=ab+b, 此时,
= g(b)=ab+b, 此时,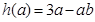
故
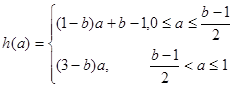 , (2分)
, (2分)因
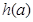 在
在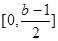 上单调递减,在
上单调递减,在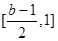 单调递增,故
单调递增,故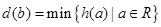 =h(
=h(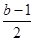 )=
)=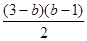 , (4分)
, (4分)故当
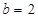 时,得
时,得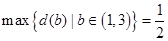 . (6分)
. (6分)(3)ⅰ)当
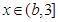 时,f(x)="b,"
时,f(x)="b," 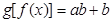
ⅱ)当
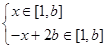 ,即
,即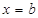 时,
时,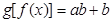
ⅲ)当
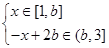 时,即
时,即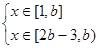 (*),(3分)
(*),(3分)①若2b-3>1即b>2, 由(*)知
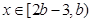 ,但此时
,但此时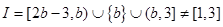 ,所以b>2不合题意。
,所以b>2不合题意。②若2b-3
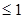 即b
即b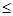 2, 由(*)知
2, 由(*)知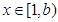 , 此时
, 此时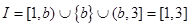
故
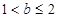 , (5分) 且
, (5分) 且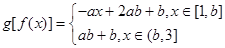
于是,当
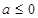 时,
时,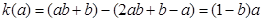
当
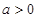 时,
时,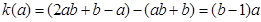
即
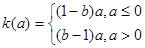 (7分)
(7分)从而可得当a=0时,
 ="0. " (8分)
="0. " (8分)略

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
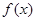 满足
满足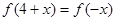 ,且
,且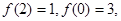 若
若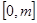 上有最小值1,最大值3,则实数
上有最小值1,最大值3,则实数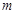 的取值范围是
的取值范围是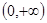
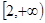
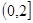
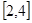
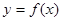 是定义在R上以
是定义在R上以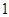 为周期的函数,若
为周期的函数,若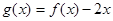 在区间
在区间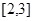 上的值域为
上的值域为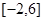 ,则函数
,则函数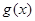 在
在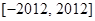 上的值域为
上的值域为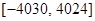
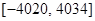
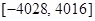
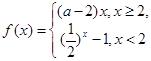 是
是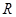 上的单调递减函数,则实数
上的单调递减函数,则实数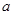 的取值范围为( )
的取值范围为( )

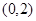

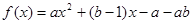 ,不等式
,不等式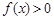 的解集是
的解集是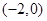 。(1)求
。(1)求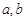 的值;(2)求函数
的值;(2)求函数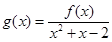 在
在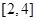 上的最大值和最小值。
上的最大值和最小值。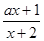 在区间(-2,+∞)上为增函数,那么实数a的取值范围为( )
在区间(-2,+∞)上为增函数,那么实数a的取值范围为( )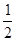
 满足对任意的
满足对任意的 成立,那么a的取值范围是( )
成立,那么a的取值范围是( )
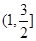
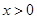 ,函数
,函数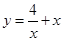 的最小值是 ********
的最小值是 ******** 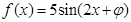 ,若对任意x∈R,都有
,若对任意x∈R,都有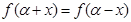 ,则
,则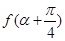 =____.
=____.