题目内容
(本小题满分14分)
设函数f(x)=tx2+2t2x+t-1(t∈R,t>0).
(1)求f(x)的最小值s(t);
(2)若s(t)<-2t+m对t∈(0,2)时恒成立,求实数m的取值范围.
设函数f(x)=tx2+2t2x+t-1(t∈R,t>0).
(1)求f(x)的最小值s(t);
(2)若s(t)<-2t+m对t∈(0,2)时恒成立,求实数m的取值范围.
解:(1)∵f(x)=tx2+2t2x+t-1
=t(x+t)2-t3+t-1(t∈R,t>0),
 3分
3分
∴当x=-t时,f(x)取得最小值f(-t)=-t3+t-1,
即s(t)=-t3+t-1.
 6分
6分
(2)令h(t)=s(t)-(-2t+m)=-t3+3t-1-m.
由h′(t)=-3t2+3=0,
 8分
8分
得t=1或t=-1(舍去),则有
 10分
10分
∴h(t)在(0,2)内有最大值1-m, 
 12分
12分
∴s(t)<-2t+m对t∈(0,2)时恒成立等价于h(t)<0恒成立,
即1-m<0,∴m>1.
 14分
14分
=t(x+t)2-t3+t-1(t∈R,t>0),

 3分
3分∴当x=-t时,f(x)取得最小值f(-t)=-t3+t-1,
即s(t)=-t3+t-1.

 6分
6分(2)令h(t)=s(t)-(-2t+m)=-t3+3t-1-m.
由h′(t)=-3t2+3=0,

 8分
8分得t=1或t=-1(舍去),则有

 10分
10分| t | (0,1) | 1 | (1,2) |
| h′(t) | + | 0 | - |
| h(t) | 增 | 极大值 | 减 |

 12分
12分∴s(t)<-2t+m对t∈(0,2)时恒成立等价于h(t)<0恒成立,
即1-m<0,∴m>1.

 14分
14分略

练习册系列答案
相关题目
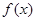 满足
满足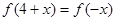 ,且
,且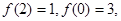 若
若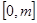 上有最小值1,最大值3,则实数
上有最小值1,最大值3,则实数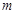 的取值范围是
的取值范围是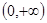
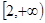
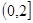
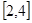
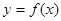 在定义域内单调,且用二分法探究知道
在定义域内单调,且用二分法探究知道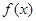 在定义域内的零点同时在
在定义域内的零点同时在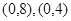 ,
,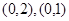 内,那么下列命题中正确的是( )
内,那么下列命题中正确的是( )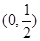 内有零点
内有零点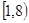 上无零点
上无零点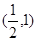 内有零点
内有零点 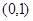 上有多个零点
上有多个零点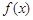 的定义域为
的定义域为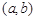 ,且对其内任意实数
,且对其内任意实数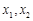 均有:
均有: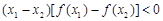 ,则
,则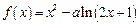 (
(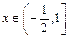 ,
,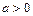 ).
). 在其定义域内是减函数,求
在其定义域内是减函数,求 的取值范围;
的取值范围;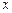 的值,并证明你的结论.
的值,并证明你的结论.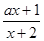 在区间(-2,+∞)上为增函数,那么实数a的取值范围为( )
在区间(-2,+∞)上为增函数,那么实数a的取值范围为( )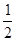
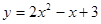

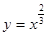

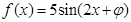 ,若对任意x∈R,都有
,若对任意x∈R,都有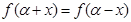 ,则
,则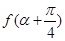 =____.
=____.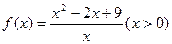 ,当
,当 ,时,函数
,时,函数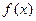 有最小值,
有最小值,