题目内容
【题目】已知二次函数![]() 的图象过点(1,13),且函数对称轴方程为
的图象过点(1,13),且函数对称轴方程为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)设函数![]() ,求
,求![]() 在区间
在区间![]() 上的最小值
上的最小值![]()
【答案】(1) ![]() ,(2)
,(2) 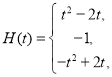
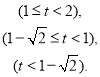
【解析】
(1)由f(x)的对称轴方程以及图象过点(1,13),求出b、c的值,从而写出f(x)的解析式;
(2)化函数g(x)为分段函数,画出函数的图象,结合图象,求出g(x)在区间[t,2]上的最小值H(t).
(1)∵f(x)=x2+bx+c的对称轴方程为![]() ,
,
∴b=1;
又f(x)=x2+bx+c的图象过点(1,13),
∴1+b+c=13,∴c=11;
∴f(x)的解析式为f(x)=x2+x+11.
(2)∵函数g(x)=[f(x)﹣x2﹣13]|x|
=[(x2+x+11)﹣x2﹣13]|x|
=(x﹣2)|x|
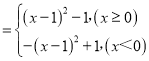 ,
,
画出函数图象,如图:
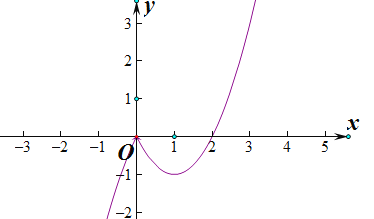
令![]() ,解得
,解得![]() 或
或![]() (舍)
(舍)
∴当1≤t<2时,g(x)min=t2﹣2t;
当![]() 时,g(x)min=﹣1;
时,g(x)min=﹣1;
当![]() 时,
时,![]() .
.
∴综上,H(t)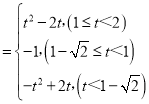 .
.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目