题目内容
【题目】已知正方形![]() 的边长为
的边长为![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起,使平面
折起,使平面![]() 平面
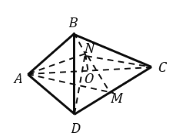
平面![]() ,得到如图所示的三棱锥
,得到如图所示的三棱锥![]() ,若
,若![]() 为
为![]() 边的中点,
边的中点,![]() 分别为
分别为![]() 上的动点(不包括端点),且
上的动点(不包括端点),且![]() ,设
,设![]() ,则三棱锥
,则三棱锥![]() 的体积取得最大值时,三棱锥
的体积取得最大值时,三棱锥![]() 的内切球的半径为_______.
的内切球的半径为_______.
【答案】![]()
【解析】
先根据条件得到BO⊥平面ACD;进而求出三棱锥N﹣AMC的体积的表达式,即可求出结论.
因为正方形ABCD的边长为2![]() ,
,
所以:AC=4
又平面ABC⊥平面ACD,O为AC边的中点
∴BO⊥AC;
所以BO⊥平面ACD
∴三棱锥N﹣AMC的体积
y=f(x)=![]() S△AMCNO
S△AMCNO
=![]() ×
×![]() ACCMsin∠ACMNO
ACCMsin∠ACMNO
=![]() ×
×![]() ×4x
×4x![]() ×(2﹣x)
×(2﹣x)
=![]() (﹣x2+2x)
(﹣x2+2x)
=﹣![]() (x﹣1)2+
(x﹣1)2+![]()
当x=1即![]() 时,三棱锥
时,三棱锥![]() 的体积取得最大值
的体积取得最大值![]()
设内切球半径为r
此时![]()
解得r=![]()
故答案为:![]()

练习册系列答案
相关题目
【题目】经销商小王对其所经营的某一型号二手汽车的使用年数![]() (0<
(0<![]() ≤10)与销售价格
≤10)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(Ⅰ)试求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(附:回归方程![]() 中,
中,
(Ⅱ)已知每辆该型号汽车的收购价格为![]() 万元,根据(Ⅰ)中所求的回归方程,
万元,根据(Ⅰ)中所求的回归方程,
预测![]() 为何值时,小王销售一辆该型号汽车所获得的利润
为何值时,小王销售一辆该型号汽车所获得的利润![]() 最大.
最大.



