题目内容
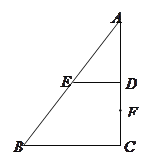
【题目】如果有一天我们分居异面直线的两头,那我一定穿越时空的阻隔,画条公垂线向你冲来,一刻也不愿逗留.如图1所示,在梯形![]() 中,
中,![]() //
//![]() ,且
,且![]() ,
,![]() ,分别延长两腰交于点
,分别延长两腰交于点![]() ,点
,点![]() 为线段
为线段![]() 上的一点,将
上的一点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2所示.
,如图2所示.

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的表面积.
的表面积.
【答案】(1)见解析;(2)![]()
【解析】
⑴先证![]() 平面
平面![]() ,继而
,继而![]() ,又
,又![]() ,证得
,证得![]() 面
面![]() ,即可证得
,即可证得![]()
⑵分别计算出梯形面积和四个三角形面积即可得到表面积
(1)证明:因为∠C=90°,即AC⊥BC,且DE∥BC,

所以DE⊥AC,则DE⊥DC,DE⊥DA1,
又因为DC∩DA1=D,
所以DE⊥平面A1DC.
因为A1F平面A1DC,
所以DE⊥A1F.
又因为A1F⊥CD,CD∩DE=D,
所以A1F⊥平面BCDE,
又因为BE 平面BCDE,
所以A1F⊥BE.
(2)解:由已知DE∥BC,且DE=![]() BC,得D,E分别为AC,AB的中点,
BC,得D,E分别为AC,AB的中点,
在Rt△ABC中,![]() ,则A1E=EB=5,A1D=DC=4,
,则A1E=EB=5,A1D=DC=4,
则梯形BCDE的面积S1=![]() ×(6+3)×4=18,
×(6+3)×4=18,
四棱锥A1—BCDE的体积为V=![]() ×18×A1F=12
×18×A1F=12![]() ,即A1F=2
,即A1F=2![]() ,
,
在Rt△A1DF中,![]() ,即F是CD的中点,
,即F是CD的中点,
所以A1C=A1D=4,
因为DE∥BC,DE⊥平面A1DC,
所以BC⊥平面A1DC,所以BC⊥A1C,所以![]() ,
,
在等腰△A1BE中,底边A1B上的高为![]() ,
,
所以四棱锥A1—BCDE的表面积为
S=S1+![]() +
+![]() +
+![]()
![]()
=18+![]() ×3×4+
×3×4+![]() ×4×2
×4×2![]() +
+![]() ×6×4+
×6×4+![]() ×2
×2![]() ×2
×2![]() =36+4
=36+4![]() +2
+2![]() .
.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目