题目内容
【题目】已知函数![]()
(1)若函数![]() 在
在![]() 处有极值为10,求
处有极值为10,求![]() 的值;
的值;
(2)对任意![]() ,
,![]() 在区间
在区间![]() 单调增,求
单调增,求![]() 的最小值;
的最小值;
(3)若![]() ,且过点
,且过点![]() 能作
能作![]() 的三条切线,求
的三条切线,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)根据![]() 列方程组,解方程组求得
列方程组,解方程组求得![]() 的值.(2)依题意得
的值.(2)依题意得![]() 对
对![]() ,当
,当![]() 恒成立,构造函数
恒成立,构造函数![]() ,利用一次函数的单调性求得
,利用一次函数的单调性求得![]() .再构造函数
.再构造函数![]() ,根据二次函数的对称轴得
,根据二次函数的对称轴得![]() ,由此求得
,由此求得![]() 的最小值.(3)当
的最小值.(3)当![]() 时,
时,![]() ,设出切点的坐标,利用导数求得切线的斜率列方程并化简,构造函数记
,设出切点的坐标,利用导数求得切线的斜率列方程并化简,构造函数记![]() ,根据过点
,根据过点![]() ,能作
,能作![]() 的三条切线可知
的三条切线可知![]() 有三个零点,利用
有三个零点,利用![]() 的导数求得
的导数求得![]() 的极大值和极小值,由此列不等式组,解不等式组求得
的极大值和极小值,由此列不等式组,解不等式组求得![]() 的取值范围.
的取值范围.
解:(1)![]() ,依题意:
,依题意:
![]() ①,
①,![]() ②
②
由①②解得:![]() ,或
,或![]() ;
;
经检验当![]() 时无极值点,
时无极值点,
当![]() 时函数
时函数![]() 在
在![]() 处有极小值,故
处有极小值,故![]() ,
,
(2)![]() 对
对![]() ,当
,当![]() 恒成立
恒成立
记![]() ,
,
∴![]()
又设![]() ,
,
当![]() 时
时![]() ,
,
![]() ,∴
,∴![]() 的最小值为
的最小值为![]() ,
,
(3):当![]() 时,
时,![]() ,
,
设切点为![]() ,则切线斜率为
,则切线斜率为![]() ,
,
∴![]() ,
,
记![]() ,
,
过点![]() 能作
能作![]() 三条切线等价于
三条切线等价于![]() 有三个零点
有三个零点
![]()
|
|
|
|
| 正 | 负 | 正 |
| 增 | 减 | 增 |
令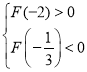 ,即
,即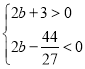 ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目