题目内容
【题目】已知函数![]() ,
,![]() .
.
![]() 若
若![]() 是函数
是函数![]() 的极值点,求曲线
的极值点,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
![]() 若函数
若函数![]() 在区间
在区间![]() 上为单调递减函数,求实数a的取值范围;
上为单调递减函数,求实数a的取值范围;
![]() 设m,n为正实数,且
设m,n为正实数,且![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
![]() 求出导函数,得到函数
求出导函数,得到函数![]() 的极值点,解得
的极值点,解得![]() ,求出切线的斜率为
,求出切线的斜率为![]() ,切点为
,切点为![]() ,然后利用点斜式求解切线方程;
,然后利用点斜式求解切线方程;![]() 由
由![]() 知
知![]() ,利用函数
,利用函数![]() 在区间
在区间![]() 上为单调递减函数,得到
上为单调递减函数,得到![]() 在区间
在区间![]() 上恒成立,推出
上恒成立,推出![]() ,设
,设![]() ,
,![]() ,
,![]() ,利用基本不等式
,利用基本不等式![]() ,再求出函数的最大值,可得实数
,再求出函数的最大值,可得实数![]() 的取值范围;
的取值范围;![]() 利用分析法证明,要证
利用分析法证明,要证![]() ,只需证
,只需证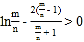 ,设
,设![]() ,
,![]() ,利用导数研究函数的单调性,可得
,利用导数研究函数的单调性,可得![]() ,从而可得结论.
,从而可得结论.
![]() ,
,![]() ./span>
./span>
![]()
![]() 是函数
是函数![]() 的极值点,
的极值点,![]() ,解得
,解得![]() ,
,
经检验,当![]() 时,
时,![]() 是函数
是函数![]() 的极小值点,符合题意
的极小值点,符合题意![]()
此时切线的斜率为![]() ,切点为
,切点为![]() ,
,
则所求切线的方程为![]()
![]() 由
由![]() 知
知![]()
因为函数![]() 在区间
在区间![]() 上为单调递减函数,
上为单调递减函数,
所以不等式![]() 在区间
在区间![]() 上恒成立
上恒成立![]()
即![]() 在区间
在区间![]() 上恒成立,
上恒成立,
当![]() 时,由
时,由![]() 可得
可得![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
当且仅当![]() 时,即
时,即![]() 时,
时,![]() ,
,
又因为函数![]() 在区间
在区间![]() 上为单调递减,在区间
上为单调递减,在区间![]() 上为单调递增,
上为单调递增,
且![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() 恒成立,
恒成立,
即![]() ,也即
,也即![]()
则所求实数a的取值范围是![]()
![]() ,n为正实数,且
,n为正实数,且![]() ,
,![]() 要证
要证![]() ,只需证
,只需证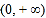
即证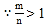 只需证
只需证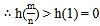
设![]() ,
,![]() ,
,
则![]() 在
在![]() 上恒成立,
上恒成立,
即函数![]() 在
在![]() 上是单调递增,
上是单调递增,
又![]() ,
,![]() ,即
,即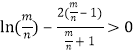 成立,
成立,
也即![]() 成立.
成立.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】某校团委对“学生性别与中学生追星是否有关”作了一次调查,利用![]() 列联表,由计算得
列联表,由计算得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
得到正确结论是( )
A. 有99%以上的把握认为“学生性别与中学生追星无关”
B. 有99%以上的把握认为“学生性别与中学生追星有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星无关”
D. 在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星有关”
【题目】经销商小王对其所经营的某一型号二手汽车的使用年数![]() (0<
(0<![]() ≤10)与销售价格
≤10)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(Ⅰ)试求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(附:回归方程![]() 中,
中,
(Ⅱ)已知每辆该型号汽车的收购价格为![]() 万元,根据(Ⅰ)中所求的回归方程,
万元,根据(Ⅰ)中所求的回归方程,
预测![]() 为何值时,小王销售一辆该型号汽车所获得的利润
为何值时,小王销售一辆该型号汽车所获得的利润![]() 最大.
最大.