题目内容
【题目】
在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于![]() .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由.
【答案】(I)![]() (II)存在点
(II)存在点![]() 使得
使得![]() 与
与![]() 的面积相等,此时点
的面积相等,此时点![]() 的坐标为
的坐标为![]() .
.
【解析】
试题(1)利用直接法设![]() ,利用直线
,利用直线![]() 与
与![]() 的斜率之积等于
的斜率之积等于![]() ,得到关于
,得到关于![]() 的方程,求得其轨迹方程;(2)根据题意设
的方程,求得其轨迹方程;(2)根据题意设![]()
![]() ,点
,点![]() 的坐标分别为
的坐标分别为![]() 三个点的坐标,再利用三角形的面积公式和点到直线的距离公式,求得
三个点的坐标,再利用三角形的面积公式和点到直线的距离公式,求得![]() 和
和![]() 的面积,利用
的面积,利用![]()
![]() ,进而得到关于
,进而得到关于![]() 的方程,求得点
的方程,求得点![]() 的坐标为
的坐标为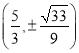 .
.
试题解析:(1)点![]() 的轨迹方程为
的轨迹方程为![]() ; 5分
; 5分
(2)设点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标分别为
的坐标分别为![]() ,
,
则直线![]() 的方程为
的方程为![]() ,
,
直线![]() 的方程为
的方程为![]() .
.
令![]() ,得
,得![]() ,
,
于是![]() 的面积
的面积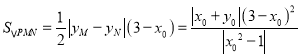 , 8分
, 8分
直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
于是![]() 的面积
的面积![]()
![]() , 10分
, 10分
当![]()
![]() 时,得
时,得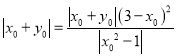 ,
,
又![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
故存在点![]() 使得
使得![]() 与
与![]() 的面积相等,
的面积相等,
此时点![]() 的坐标为
的坐标为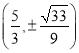 . 12分
. 12分

【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程![]() ,变量x增加一个单位时,y平均增加5个单位;
,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程![]() 必过
必过![]() ;
;
④在一个![]() 列联表中,由计算得是
列联表中,由计算得是![]() ,则有
,则有![]() 的把握确认这两个变量间有关系.
的把握确认这两个变量间有关系.
其中错误的个数是( )
本题可以参考独立性检验临界值表:
| 0.05 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.0B.1C.2D.3
【题目】调查某校高三年级男生的身高,随机抽取40名高三男生,实测身高数据(单位:cm)如下:
171 | 163 | 163 | 166 | 166 | 168 | 168 | 160 | 168 | 165 |
171 | 169 | 167 | 169 | 151 | 168 | 170 | 168 | 160 | 174 |
165 | 168 | 174 | 159 | 167 | 156 | 157 | 164 | 169 | 180 |
176 | 157 | 162 | 161 | 158 | 164 | 163 | 163 | 167 | 161 |
(1)作出频率分布表;
(2)画出频率分布直方图.