Question

【题目】若对任意的正整数，总存在正整数，使得数列的前项和，则称数列是“回归数列”.

（1）前项和为的数列是否是“回归数列”？并请说明理由；

（2）设是等差数列，首项，公差，若是“回归数列”，求的值；

（3）是否对任意的等差数列，总存在两个“回归数列”和，使得（）成立，请给出你的结论，并说明理由.

Answer 1

【答案】（1）是；（2）；（3）存在，理由见解析.

【解析】

（1）由题意，根据数列中与，分别的奥和时，对任意的存在正整数使得成立，解得结论；

（2）因为是等差数列，首项，公差，则对任意的存在正整数使得成立，现求得当时，得到，再验证时，对任意的存在正整数使得成立，即可得到结论。

（3）由（2）知，可以构造一个回归的等差数列，验证时，得到，使得成立，进而对于对任意等差数列，得到，使得成立，即可得到答案。

（1）

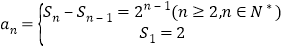
显然

时，存在正整数使得成立符合题意

时，对任意的存在正整数使得成立

（2）因为是等差数列，首项，公差

所以对任意的存在正整数使得成立

当时，公差，所以正整数只能是1，所以

验证：时，对任意的存在正整数使得成立

（3）由（2）知，可以构造一个回归的等差数列

验证：

时，是奇数，是偶数，是偶数，是奇数，

对任意的存在正整数，使得成立

对任意的一个等差数列，

一定得到

是常数，是等差数列，首项为0

任意的，它的前项和，假设它是回归数列，则存在正整数使2得成立，成立

解得