Question

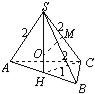
【题目】已知三棱锥S-ABC的底面是以AB为斜边的等腰直角三角形，SA=SB= SC=2，AB=2，设S、A、B、C四点均在以O为球心的某个球面上。则点O到平面ABC的距离为________________。

Answer 1

【答案】

【解析】

试题根据三棱锥S﹣ABC的底面是以AB为斜边的等腰直角三角形，SA=SB=SC，可得S在面ABC上的射影为AB中点H，SH⊥平面ABC，在面SHC内作SC的垂直平分线MO与SH交于O，则O为SABC的外接球球心，OH为O与平面ABC的距离，由此可得结论．

解：∵三棱锥S﹣ABC的底面是以AB为斜边的等腰直角三角形，SA=SB=SC，

∴S在面ABC上的射影为AB中点H，∴SH⊥平面ABC．

∴SH上任意一点到A、B、C的距离相等．

∵SH=，CH=1，在面SHC内作SC的垂直平分线MO与SH交于O，则O为SABC的外接球球心．

∵SC=2

∴SM=1，∠OSM=30°

∴SO=，∴OH=，即为O与平面ABC的距离．

故答案为：