题目内容
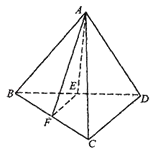
【题目】已知四棱锥P﹣ABCD中,底面ABCD为平行四边形,点M,N,Q分别在PA,BD,PD上.
(1)若PM:MA=BN:ND=PQ:QD,求证:平面MNQ∥平面PBC.
(2)若Q满足PQ:QD=2,则M点满足什么条件时,BM∥面AQC.
【答案】(1)证明见解析(2)M为PA的中点
【解析】
![]() 利用线面平行的判定定理证明MQ∥平面PBC, QN∥平面PBC,然后面面平行的判定定理即可证明;
利用线面平行的判定定理证明MQ∥平面PBC, QN∥平面PBC,然后面面平行的判定定理即可证明;
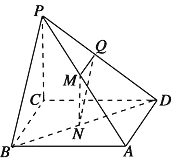
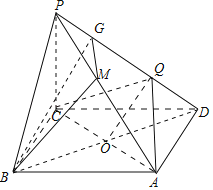
![]() 连接AC,交BD于O,连接OQ,取PQ的中点G,连接BG,利用线面平行的判定定理可证BG∥平面AQC,取PA的中点M,连接GM,同理可证, GM∥平面AQC,再由面面平行的判定定理证明平面BGM∥平面AQC,再由面面平行的性质即可得证.
连接AC,交BD于O,连接OQ,取PQ的中点G,连接BG,利用线面平行的判定定理可证BG∥平面AQC,取PA的中点M,连接GM,同理可证, GM∥平面AQC,再由面面平行的判定定理证明平面BGM∥平面AQC,再由面面平行的性质即可得证.
(1)证明:∵PM:MA=PQ:QD.
∴QM∥AD,∵AD∥BC,∴QM∥BC,
∵![]() 平面PBC,BC平面PBC,
平面PBC,BC平面PBC,
∴MQ∥平面PBC,
∵BN:ND=PQ:QD.∴QN∥PB,
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() QN∥平面PBC,
QN∥平面PBC,
∵QM∩QN=Q,∴平面MNQ∥平面PBC;
(2)当M点为PA的中点时,BM∥面AQC
证明如下:连接AC,交BD于O,连接OQ,
取PQ的中点G,连接BG,则BG∥OQ,
∵OQ平面AQC,BG平面AQC,∴BG∥平面AQC,
取PA的中点M,连接GM,则GM∥AQ,
∵AQ平面AQC,GM平面AQC,∴GM∥平面AQC,
又BG∩GM=G,∴平面BGM∥平面AQC,
则BM∥面AQC,此时M为PA的中点.

 名校课堂系列答案
名校课堂系列答案【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式: 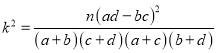 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |