题目内容
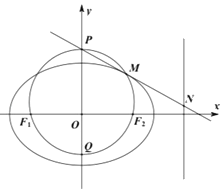
【题目】如图,点M在椭圆![]() 1(0<b
1(0<b![]() )上,且位于第一象限,F1,F2为椭圆的两个焦点,过F1,F2,M的圆与y轴交于点P,Q(P在Q的上方),|OP||OQ|=1.
)上,且位于第一象限,F1,F2为椭圆的两个焦点,过F1,F2,M的圆与y轴交于点P,Q(P在Q的上方),|OP||OQ|=1.
(Ⅰ)求b的值;
(Ⅱ)直线PM与直线x=2交于点N,试问,在x轴上是否存在定点T,使得![]()
![]() 为定值?若存在,求出点T的坐标与该定值;若不存在,请说明理由.
为定值?若存在,求出点T的坐标与该定值;若不存在,请说明理由.
【答案】(Ⅰ)1(Ⅱ)存在定点T(1,0),使得![]()
![]() 为定值0.
为定值0.
【解析】
(I)设圆心![]() .则圆的方程为:
.则圆的方程为:![]() ,令
,令![]() ,得:
,得:![]() ,即可得出
,即可得出![]() ,进而得出.
,进而得出.
(II)设![]() .将
.将![]() 代入圆与椭圆的方程,可得
代入圆与椭圆的方程,可得![]() 坐标,可得直线
坐标,可得直线![]() 的方程,设
的方程,设![]() ,可得
,可得![]()
![]() ,即可得出.
,即可得出.
(I)设圆心(0,t).则圆的方程为:x2+(y﹣t)2=c2+t2.
令x=0,得:y2﹣2ty﹣c2=0(*),
∴|OP||OQ|=|yPyQ|=c2=1.
∴b=a2﹣c2=1.
(II)设M(x0,y0).![]()
将M(x0,y0)代入圆与椭圆的方程,可得:![]() 2ty0﹣1=0,
2ty0﹣1=0,![]() 2
2![]() 2,消去x0,
2,消去x0,
得t![]() ,代入(*)得:y2
,代入(*)得:y2![]() 1=0,
1=0,
即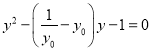 ,所以
,所以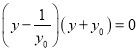
过F1,F2,M的圆与y轴交于点P,Q(P在Q的上方).
所以yP![]() ,
,![]() .
.
则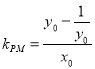 .
.
则直线![]() 的方程为:y
的方程为:y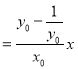
![]() ,
,
由直线PM与![]() 的交点为
的交点为![]() .
.
所以在直线PM的方程中,令![]() 得,
得,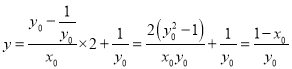 .
.
得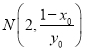
设T(d,0),![]()
![]() (x0﹣d,y0)(2﹣d,
(x0﹣d,y0)(2﹣d,![]() )
)
=(x0﹣d)(2﹣d)+1﹣x0=(1﹣d)x0﹣d(2﹣d)+1.
要使得![]()
![]() 为定值,即与M的坐标无关.
为定值,即与M的坐标无关.
当d=1时,![]()
![]() 0为定值.
0为定值.
存在定点T(1,0),使得![]()
![]() 为定值0.
为定值0.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案【题目】在创建“全国文明卫生城市”过程中,某市“创城办”为了调查市民对创城工作的了解情况,进行了一次创城知识问卷调查(一位市民只能参加一次).通过随机抽样,得到参加问卷调查的![]() 人的得分(满分100分)统计结果如下表所示:
人的得分(满分100分)统计结果如下表所示:
组别 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)由频数分布表可以大致认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这
近似为这![]() 人得分的平均值(同一组中的数据用该组区间的中点值作代表),利用该正态分布,求
人得分的平均值(同一组中的数据用该组区间的中点值作代表),利用该正态分布,求![]()
(2)在(1)的条件下,“创城办”为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于![]() 的可以获赠
的可以获赠![]() 次随机话费,得分低于
次随机话费,得分低于![]() 的可以获赠
的可以获赠![]() 次随机话费;
次随机话费;
②每次获赠的随机话费和对应的概率为:
赠送话费的金额(单位:元) |
|
|
概率 |
|
|
现有市民甲参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列与均值.
的分布列与均值.
附:参考数据与公式![]()
若![]() ,则
,则![]() =0.9544,
=0.9544,![]()