题目内容
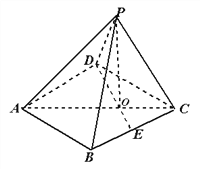
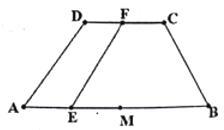
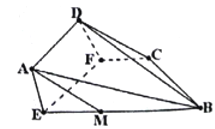
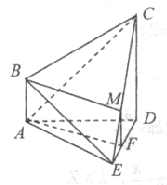
【题目】如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(I)求棱锥C-ADE的体积;
(II)求证:平面ACE⊥平面CDE;
(III)在线段DE上是否存在一点F,使AF∥平面BCE?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

【答案】(Ⅰ) ![]() ;(Ⅱ)证明见解析;(Ⅲ)答案见解析.
;(Ⅱ)证明见解析;(Ⅲ)答案见解析.
【解析】试题分析:(I)在![]() 中,
中, ![]() ,可得
,可得![]() ,由于
,由于![]() 平面
平面![]() ,可得
,可得![]() ;(II)由
;(II)由![]() 平面
平面![]() ,可得
,可得![]() ,进而得到
,进而得到![]() 平面
平面![]() ,即可证明平面
,即可证明平面![]() 平面
平面![]() ;(III)在线段
;(III)在线段![]() 上存在一点
上存在一点![]() ,使
,使![]() 平面
平面![]() ,
, ![]() .设
.设![]() 为线段
为线段![]() 上的一点,且
上的一点,且![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,由线面垂直的性质可得:
,由线面垂直的性质可得: ![]() .可得四边形
.可得四边形![]() 是平行四边形,于是
是平行四边形,于是![]() ,即可证明
,即可证明![]() 平面
平面![]()
试题解析:(I)在Rt△ADE中, ![]() ,因为CD⊥平面ADE,
,因为CD⊥平面ADE,
所以棱锥C-ADE的体积为![]() .
.
(II)因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .又因为
.又因为![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()
(III)在线段![]() 上存在一点F,且
上存在一点F,且![]() ,使
,使![]() 平面
平面![]() .
.
解:设![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,则
,则![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ,又因为
,又因为![]()
所以![]() ,
, ![]() ,所以四边形
,所以四边形![]() 是平行四边形,则
是平行四边形,则![]() .
.
又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.

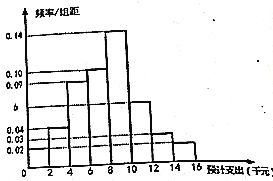
【题目】随着网络时代的进步,流量成为手机的附带品,人们可以利用手机随时随地的浏览网页,聊天,看视频,因此,社会上产生了很多低头族.某研究人员对该地区18∽50岁的5000名居民在月流量的使用情况上做出调查,所得结果统计如下图所示:
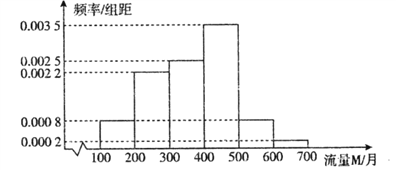
(Ⅰ)以频率估计概率,若在该地区任取3位居民,其中恰有![]() 位居民的月流量的使用情况
位居民的月流量的使用情况
在300M∽400M之间,求![]() 的期望
的期望![]() ;
;
(Ⅱ)求被抽查的居民使用流量的平均值;
(Ⅲ)经过数据分析,在一定的范围内,流量套餐的打折情况![]() 与其日销售份数
与其日销售份数![]() 成线性相关
成线性相关
关系,该研究人员将流量套餐的打折情况![]() 与其日销售份数
与其日销售份数![]() 的结果统计如下表所示:
的结果统计如下表所示:
折扣 | 1折 | 2折 | 3折 | 4折 | 5折 |
销售份数 | 50 | 85 | 115 | 140 | 160 |
试建立![]() 关于
关于![]() 的的回归方程.
的的回归方程.
附注:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
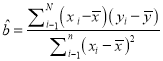 ,
, ![]()