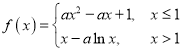题目内容
【题目】已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),点
为参数),点![]() 时曲线
时曲线![]() 上两点,点
上两点,点![]() 的极坐标分别为
的极坐标分别为![]() ,
,![]() .
.
(1)写出曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ,(2)6
,(2)6
【解析】
(1)消去参数![]() ,把曲线
,把曲线![]() 的参数方程化为普通方程,再由公式
的参数方程化为普通方程,再由公式![]() ,把曲线
,把曲线![]() 的普通方程化为极坐标方程;
的普通方程化为极坐标方程;
(2)方法1:由![]() 两点的极坐标,得出
两点的极坐标,得出![]() ,判定
,判定![]() 为直径,求出
为直径,求出![]() ;
;
方法2:把![]() 化为直角坐标的点的坐标,求出
化为直角坐标的点的坐标,求出![]() 两点间距离
两点间距离![]() .
.
(1)![]() 曲线
曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),
为参数),
消去参数![]() ,化为普通方程是
,化为普通方程是![]() ;
;
由![]() ,(
,(![]() 为参数),
为参数),
![]() 曲线
曲线![]() 的普通方程可化为极坐标
的普通方程可化为极坐标![]() ,(
,(![]() 为参数).
为参数).
(2)方法1:由![]() 是圆
是圆![]() 上的两点,
上的两点,
且知![]() ,
,
∴![]() 为直径,
为直径,![]() .
.
方法2:由两点![]() 化为直角坐标中点的坐标是:
化为直角坐标中点的坐标是:
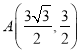 ,
,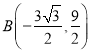 ,
,
∴![]() 、
、![]() 两点间的距离为:
两点间的距离为:![]() .
.

练习册系列答案
相关题目
【题目】为检查某工厂所生产的8万台电风扇的质量,抽查了其中20台的无故障连续使用时限(单位:小时) 如下:
248 256 232 243 188 268 278 266 289 312
274 296 288 302 295 228 287 217 329 283
分组 | 频数 | 频率 | 频率/组距 |
| |||
| |||
| |||
| |||
| |||
| |||
| |||
| |||
总计 | 0.05 |
(1)完成频率分布表,并作出频率分布直方图;
(2)估计8万台电风扇中有多少台无故障连续使用时限不低于280小时;
(3)用组中值(同一组中的数据在该组区间的中点值)估计样本的平均无故障连续使用时限.