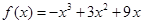题目内容
(本小题满分14分)
已知函数 的单调递增区间为
的单调递增区间为 ,
,
(Ⅰ)求证: ;
;
(Ⅱ)当 取最小值时,点
取最小值时,点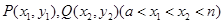 是函数
是函数 图象上的两点,若存在
图象上的两点,若存在 使得
使得 ,求证:
,求证:
已知函数
 的单调递增区间为
的单调递增区间为 ,
,(Ⅰ)求证:
 ;
;(Ⅱ)当
 取最小值时,点
取最小值时,点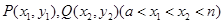 是函数
是函数 图象上的两点,若存在
图象上的两点,若存在 使得
使得 ,求证:
,求证:
见解析。
本试题主要是考查了导数在研究函数中的运用。
(1)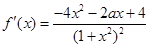 ,依题意
,依题意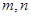 是方程
是方程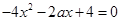 的两根有:
的两根有: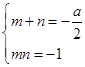
(2)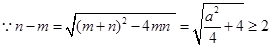
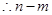 取最小值时,
取最小值时,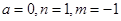 ,
,
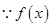 在
在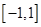 上是增函数,
上是增函数, ,
,
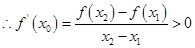 ,从而
,从而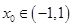 ,结合函数单调性得到证明。
,结合函数单调性得到证明。
解:(Ⅰ)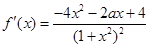 ………………………2分
………………………2分
依题意 是方程
是方程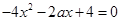 的两根有:
的两根有: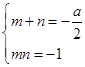 ………………………………4分
………………………………4分
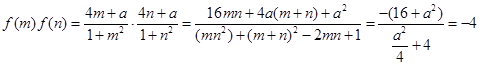 ……6分
……6分
(Ⅱ)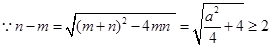
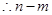 取最小值时,
取最小值时,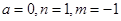 ,…………………………7分
,…………………………7分
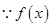 在
在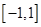 上是增函数,
上是增函数, ,
,
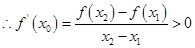 ,从而
,从而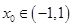 ……………………………8分
……………………………8分
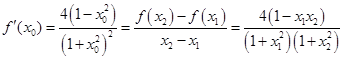
即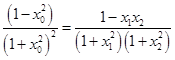
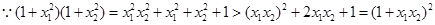
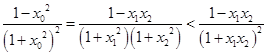 …………10分
…………10分
考虑函数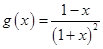 ,因
,因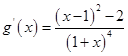 ,故当
,故当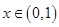 时,有
时,有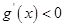 ,
,
所以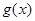 是
是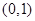 上是减函数.
上是减函数.
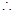 由
由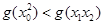 ,得
,得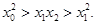
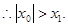 …………………12分
…………………12分
由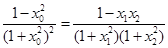 及
及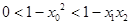 得
得
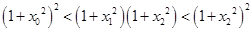 故
故 ,即
,即 .
.
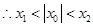 ……………………14分
……………………14分
(1)
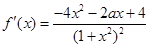 ,依题意
,依题意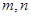 是方程
是方程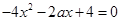 的两根有:
的两根有: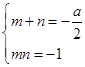
(2)
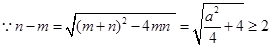
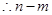 取最小值时,
取最小值时,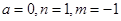 ,
,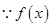 在
在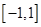 上是增函数,
上是增函数, ,
,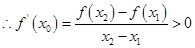 ,从而
,从而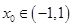 ,结合函数单调性得到证明。
,结合函数单调性得到证明。解:(Ⅰ)
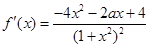 ………………………2分
………………………2分依题意
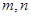 是方程
是方程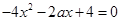 的两根有:
的两根有: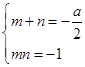 ………………………………4分
………………………………4分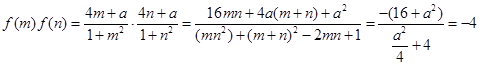 ……6分
……6分(Ⅱ)
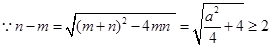
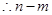 取最小值时,
取最小值时,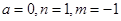 ,…………………………7分
,…………………………7分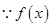 在
在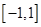 上是增函数,
上是增函数, ,
,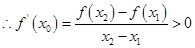 ,从而
,从而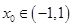 ……………………………8分
……………………………8分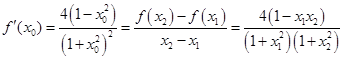
即
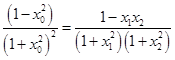
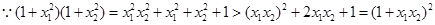
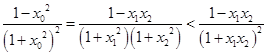 …………10分
…………10分考虑函数
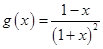 ,因
,因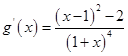 ,故当
,故当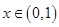 时,有
时,有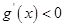 ,
,所以
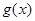 是
是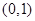 上是减函数.
上是减函数. 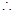 由
由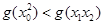 ,得
,得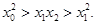
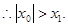 …………………12分
…………………12分由
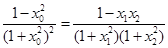 及
及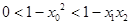 得
得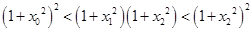 故
故 ,即
,即 .
.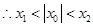 ……………………14分
……………………14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
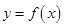 是函数
是函数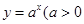 且
且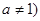 的反函数,且
的反函数,且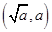 ,则
,则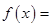
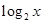
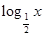
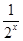
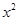
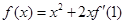 ,
,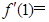 .
.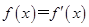 的较大实数根叫做函数
的较大实数根叫做函数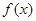 的“轻松点”,若函数
的“轻松点”,若函数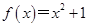 ,
,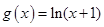 ,
,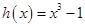 的“轻松点”分别为
的“轻松点”分别为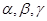 ,则
,则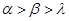 B.
B.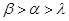 C.
C.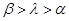 D.
D.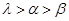
 为实数,函数
为实数,函数 。
。 ,求
,求 的最小值
的最小值  ,直接写出(不需要给出演算步骤)不等式
,直接写出(不需要给出演算步骤)不等式 的解集。
的解集。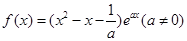 .
.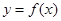 在点
在点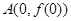 处的切线方程;
处的切线方程;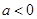 时,求函数
时,求函数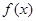 的单调区间.
的单调区间.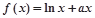
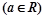 .
.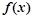 的单调区间;
的单调区间;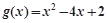 ,若对任意
,若对任意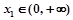 ,均存在
,均存在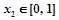 ,使得
,使得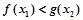 ,求a的取值范围.
,求a的取值范围. 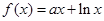
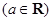 .
.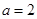 ,求曲线
,求曲线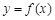 在
在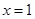 处切线的斜率;
处切线的斜率;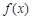 的单调区间;
的单调区间;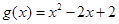 ,若对任意
,若对任意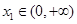 ,均存在
,均存在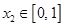 ,使得
,使得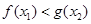 ,求
,求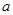 的取值范围。
的取值范围。