题目内容
【题目】某市教育局委托调查机构对本市中小学学校使用“微课掌上通”满意度情况进行调查.随机选择小学和中学各50所学校进行调查,调查情况如表:
评分等级 | ☆ | ☆☆ | ☆☆☆ | ☆☆☆☆ | ☆☆☆☆☆ |
小学 | 2 | 7 | 9 | 20 | 12 |
中学 | 3 | 9 | 18 | 12 | 8 |
(备注:“☆”表示评分等级的星级,例如“☆☆☆”表示3星级.)
(1)从评分等级为5星级的学校中随机选取两所学校,求恰有一所学校是中学的概率;
(2)规定:评分等级在4星级以上(含4星)为满意,其它星级为不满意.完成下列2×2列联表并帮助判断:能否在犯错误的概率不超过0.05的前提下认为使用是否满意与学校类别有关系?
学校类型 | 满意 | 不满意 | 总计 |
小学 | 50 | ||
中学 | 50 | ||
总计 | 100 |
【答案】
(1)解:因为从5星级的20所学校中随机选取2所,共有 ![]() =190种结果,
=190种结果,
其中恰有1所学校是中学的共有 ![]()
![]() =96种结果,;
=96种结果,;
故所求概率为P= ![]() =
= ![]()
(2)解:由2×2列联表:
学校类型 | 满意 | 不满意 | 总计 |
小学 | 32 | 18 | 50 |
中学 | 20 | 30 | 50 |
总计 | 52 | 48 | 100 |
经计算K2的观测值:K2= ![]() ≈5.769>3.841;
≈5.769>3.841;
所以在犯错误的概率不超过0.05的前提下认为使用满意与学校类型有关系.
【解析】(1)由古典概型公式,分别求得从5星级的20所学校中随机选取2所总事件个数m及恰有1所学校是中学的事件个数n,P= ![]() =
= ![]() ,代入即可求得x和y的值;(2)根据所给数据,可得2×2列联表,求出K2 , 与临界值比较,在犯错误的概率不超过0.05的前提下认为使用满意与学校类型有关系.
,代入即可求得x和y的值;(2)根据所给数据,可得2×2列联表,求出K2 , 与临界值比较,在犯错误的概率不超过0.05的前提下认为使用满意与学校类型有关系.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】已知某产品的历史收益率的频率分布直方图如图所示:
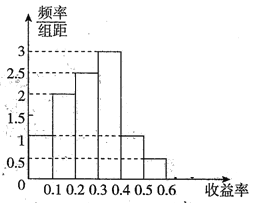
(1)试计算该产品收益率的中位数;
(2)若该产品的售价![]() (元)与销量
(元)与销量![]() (万件)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组
(万件)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组![]() 与
与![]() 的对应数据:
的对应数据:
售价 | 25 | 30 | 38 | 45 | 52 |
销量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
据此计算出的回归方程为![]() ,求
,求![]() 的值;
的值;
(3)若从上述五组销量中随机抽取两组,求两组销量中恰有一组超过6万件的概率.
【题目】对甲、乙的学习成绩进行抽样分析,各抽五门功课,得到的观测值如表:
甲 | 60 | 80 | 70 | 90 | 70 |
乙 | 80 | 60 | 70 | 80 | 75 |
问:甲、乙谁的平均成绩较好?谁的各门功课发展较平衡?( )
A.甲的平均成绩较好,乙的各门功课发展较平衡
B.甲的平均成绩较好,甲的各门功课发展较平衡
C.乙的平均成绩较好,甲的各门功课发展较平衡
D.乙的平均成绩较好,乙的各门功课发展较平衡