题目内容
【题目】函数y=ax3﹣x2+cx(a≠0)的图象如图所示,它与x轴仅有两个公共点O(0,0)与A(xA , 0)(xA>0); 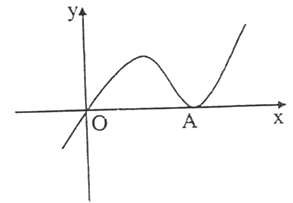
(1)用反证法证明常数c≠0;
(2)如果 ![]() ,求函数的解析式.
,求函数的解析式.
【答案】
(1)解:假设c=0,则y=ax3﹣x2=x2(ax﹣1);
∴ 这与图象所给的:
当0<x<xA时,f(x)>0矛盾,∴c≠0
(2)解:由(1)知c≠0,∴y=x(ax2﹣x+c)
∵图象与x轴仅有两个公共点,
∴方程ax2﹣x+c=0(a≠0)有二等根 .
由韦达定理 ,∴ ,∴
【解析】分析:(1)根据反证明法的证明方法,先假设c=0,则y=ax3﹣x2=x2(ax﹣1),这与图象所给的矛盾,从而得出c≠0;(2)由(1)知c≠0,得出y=x(ax2﹣x+c),图象与x轴仅有两个公共点,得出方程ax2﹣x+c=0(a≠0)有二等根 ![]() .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】海南中学对高二学生进行心理障碍测试得到如下列联表:
焦虑 | 说谎 | 懒惰 | 总计 | |
女生 | 5 | 10 | 15 | 30 |
男生 | 20 | 10 | 50 | 80 |
总计 | 25 | 20 | 65 | 110 |
试说明在这三种心理障碍中哪一种与性别关系最大?
参考数据:K2= ![]()
P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10.828 |
【题目】函数f(x)的定义域为(﹣∞,a)∪(a,+∞),f(x)≥0的解集为M,f(x)<0的解集为N,则下列结论正确的是( )
A.M=CRN
B.CRM∩CRN=
C.M∪N=R
D.CRM∪CRN=R
【题目】某市教育局委托调查机构对本市中小学学校使用“微课掌上通”满意度情况进行调查.随机选择小学和中学各50所学校进行调查,调查情况如表:
评分等级 | ☆ | ☆☆ | ☆☆☆ | ☆☆☆☆ | ☆☆☆☆☆ |
小学 | 2 | 7 | 9 | 20 | 12 |
中学 | 3 | 9 | 18 | 12 | 8 |
(备注:“☆”表示评分等级的星级,例如“☆☆☆”表示3星级.)
(1)从评分等级为5星级的学校中随机选取两所学校,求恰有一所学校是中学的概率;
(2)规定:评分等级在4星级以上(含4星)为满意,其它星级为不满意.完成下列2×2列联表并帮助判断:能否在犯错误的概率不超过0.05的前提下认为使用是否满意与学校类别有关系?
学校类型 | 满意 | 不满意 | 总计 |
小学 | 50 | ||
中学 | 50 | ||
总计 | 100 |