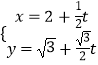题目内容
【题目】已知函数f（x）= 
在点（1，2）处的切线与f（x）的图象有三个公共点，则b的取值范围是（ ）
A.[﹣8，﹣4+2 
）
B.（﹣4﹣2 ，﹣4+2 ）
C.（﹣4+2 ，8]
D.（﹣4﹣2 ，﹣8]
【答案】D
【解析】解：当x＞0时，f（x）=x2+1，
则f′（x）=2x，
∴f′（1）=2×1=2，
则在点（1，2）处的切线方程为y=2x，
当x≤0时，y=f（x）= 
+b，
即（x+2）2+（y﹣b）2=4（y≥b）
作出函数图象如右图
随着b减小时，半圆向下移动，当点A（﹣4，b）落在切线上时，在点（1，2）处的切线与f（x）的图象有三个公共点，即b=2×（﹣4）=﹣8，
再向下移动，直到半圆与直线相切前，切线f（x）的图象有三个公共点，相切时与f（x）的图象有两个交点
即 
=2，解得b=﹣4﹣2 
＜﹣8
∴b的取值范围是（﹣4﹣2 ，﹣8]．
故选：D．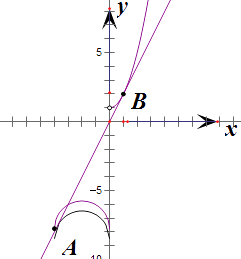
【题目】为了解某市的交通状况，现对其6条道路进行评估，得分分别为：5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如下表：
评估的平均得分 |
|
|
|
全市的总体交通状况等级 | 不合格 | 合格 | 优秀 |
（1）求本次评估的平均得分，并参照上表估计该市的总体交通状况等级；
（2）用简单随机抽样方法从这
条道路中抽取
条，它们的得分组成一个样本，求该样本的平均数与总体的平均数之差的绝对值不超过
的概率.
【题目】函数f（x）的定义域为（﹣∞，a）∪（a，+∞），f（x）≥0的解集为M，f（x）＜0的解集为N，则下列结论正确的是（ ）
A.M=CRN
B.CRM∩CRN=
C.M∪N=R
D.CRM∪CRN=R
【题目】某市教育局委托调查机构对本市中小学学校使用“微课掌上通”满意度情况进行调查．随机选择小学和中学各50所学校进行调查，调查情况如表：
评分等级 | ☆ | ☆☆ | ☆☆☆ | ☆☆☆☆ | ☆☆☆☆☆ |
小学 | 2 | 7 | 9 | 20 | 12 |
中学 | 3 | 9 | 18 | 12 | 8 |
（备注：“☆”表示评分等级的星级，例如“☆☆☆”表示3星级．）
（1）从评分等级为5星级的学校中随机选取两所学校，求恰有一所学校是中学的概率；
（2）规定：评分等级在4星级以上（含4星）为满意，其它星级为不满意．完成下列2×2列联表并帮助判断：能否在犯错误的概率不超过0.05的前提下认为使用是否满意与学校类别有关系？
学校类型 | 满意 | 不满意 | 总计 |
小学 | 50 | ||
中学 | 50 | ||
总计 | 100 |
