Question

【题目】已知函数f（x）是定义在（﹣4，4）上的奇函数，满足f（2）＝1，当﹣4＜x≤0时，有f（x）＝．

（1）求实数a，b的值；

（2）求函数f（x）在区间（0，4）上的解析式，并利用定义证明其在该区间上的单调性；

（3）解关于m的不等式f（m2+1）+>0．

Answer 1

【答案】（1）；（2），见解析；（3）{m|﹣＜m＜﹣1或1＜m＜}

【解析】

（1）因为是定义在（﹣4，4）上的奇函数，且，所以， ，列方程组求可求得；

（2）①先求在的解析式，再利用，求的解析式；②任取，且，作差，求，化简，判断的正负，得到结论.

（3）根据函数的单调性和奇偶性逐步化简求不等式.

（1）由题可知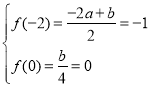，，解得；

（2）由（1）可知当时，，

当时，，，

任取，且，

∵，且，则，

于是，∴在上单调递增；

（3）∵函数是定义在（﹣4，4）上的奇函数，且在上单调递增，

则在上单调递增，∵且为奇函数，

∴，∴，解得，或，∴不等式的解集为{m|或}．