题目内容
8.已知双曲线的顶点与焦点分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
分析 根据双曲线的顶点与焦点分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的焦点与顶点,确定双曲线的顶点与焦点,再根据双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,确定双曲线的渐近线,从而求出椭圆的离心率.
解答 解:∵双曲线的顶点与焦点分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的焦点与顶点,
∴双曲线的顶点是(0,±$\sqrt{{a}^{2}-{b}^{2}}$),焦点是(0,±a),
设双曲线方程为$\frac{{y}^{2}}{{m}^{2}}-\frac{{x}^{2}}{{n}^{2}}=1$(m>0,n>0),
∴双曲线的渐近线方程为y=±$\frac{n}{m}$x,
∵m=$\sqrt{{a}^{2}-{b}^{2}}$,n2=a2-m2=b2,
∴n=b,
∵双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,
∴双曲线的渐近线方程为y=±x,
∴m=n,
∴a2-b2=b2,
∴c2=a2-c2,
∴a2=2c2,
∴a=$\sqrt{2}$c
∴e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$.
故选:C.
点评 本题以椭圆方程为载体,考查双曲线的几何性质,考查椭圆的离心率,正确运用几何量的关系是解题的关键.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
18.阅读如图所示的程序框图,若输出的数据为58,则判断框中应填入的条件为( )
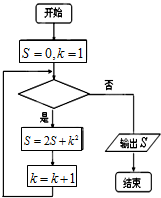

| A. | k≤3 | B. | k≤4 | C. | k≤5 | D. | k≤6 |
20.若$\frac{a}{1-i}$=$\frac{1+i}{i}$(i为虚数单位),则a的值为( )
| A. | i | B. | -i | C. | -2i | D. | 2i |
18.已知命题p:“?∈[1,e],a>lnx”,命题q:“?x∈R,x2-4x+a=0””若“p∧q”是真命题,则实数a的取值范围是( )
| A. | (1,4] | B. | (0,1] | C. | [-1,1] | D. | (4,+∞) |
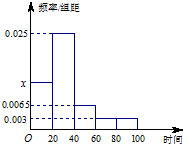 某学校随机抽取100名学生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].则该校学生上学所需时间的均值估计为33.6.(精确到1分钟)
某学校随机抽取100名学生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].则该校学生上学所需时间的均值估计为33.6.(精确到1分钟)