题目内容
5．一个几何体按比例绘制的三视图如图所示（单位：m），则该几何体的体积为（ ）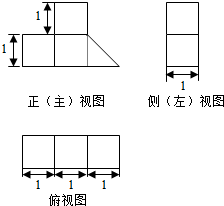
| A． | $\frac{7}{3}$ m3 | B． | $\frac{9}{2}$ m3 | C． | $\frac{9}{4}$ m3 | D． | $\frac{7}{2}$ m3 |
分析 由已知中的三视图，可知该几何体是一个以正视图为底面的七棱柱，分别计算底面面积和高，代入柱体体积公式，可得答案．
解答 解：由已知中的三视图，可知该几何体是一个以正俯视图为底面的七棱柱，
其底面面积S=$\frac{7}{2}$m2，
高h=1m，
故几何体的体积V=Sh=$\frac{7}{2}$m3，
故选：D．
点评 本题考查的知识点是简单空间图象的三视图，其中根据已知中的视图分析出几何体的形状及棱长是解答的关键．
练习册系列答案
相关题目
15．定义在区间[a，b]（b＞a）上的函数$f（x）=\frac{1}{2}sinx-\frac{{\sqrt{3}}}{2}cosx$的值域是$[-\frac{1}{2}，1]$，则b-a的最大值M和最小值m分别是（ ）
| A． | $m=\frac{π}{6}，M=\frac{π}{3}$ | B． | $m=\frac{π}{3}，M=\frac{2π}{3}$ | C． | $m=\frac{4π}{3}，M=2π$ | D． | $m=\frac{2π}{3}，M=\frac{4π}{3}$ |
20．若$\frac{a}{1-i}$=$\frac{1+i}{i}$（i为虚数单位），则a的值为（ ）
| A． | i | B． | -i | C． | -2i | D． | 2i |
10．已知函数y=ex，若f（x）的图象的一条切线经过点（-1，0），则这条切线与直线x=1及x轴所围成的三角形面积为（ ）
| A． | $\frac{2}{e}$ | B． | 1 | C． | 2 | D． | e |
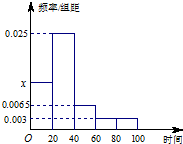某学校随机抽取100名学生调查其上学所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．则该校学生上学所需时间的均值估计为33.6．（精确到1分钟）