题目内容
17.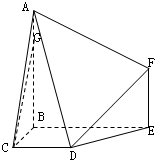 如图,在多面体ABCDEF中,BA⊥BE,BA⊥BC,BE⊥BC,AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1,G在线段AB上,且BG=3GA.
如图,在多面体ABCDEF中,BA⊥BE,BA⊥BC,BE⊥BC,AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1,G在线段AB上,且BG=3GA.(1)求证:CG∥平面ADF;
(2)求直线DE与平面ADF所成的角的正弦值;
(3)求锐二面角B-DF-A的余弦值.
分析 (1)分别取AB、AF中点M、H,连接FM、GH、DH,证明:四边形CDHG是平行四边形,可得CG∥DH,利用线面平行的判定定理证明CG∥平面ADF;
(2)建立空间直角坐标系,求出$\overrightarrow{DE}$、平面ADF的一个法向量,利用向量的夹角公式求直线DE与平面ADF所成的角的正弦值;
(3)求出平面BDF的一个法向量,利用向量的夹角公式求锐二面角B-DF-A的余弦值.
解答  (1)证明:分别取AB、AF中点M、H,连接FM、GH、DH,则有AG=GM,MF∥BE,
(1)证明:分别取AB、AF中点M、H,连接FM、GH、DH,则有AG=GM,MF∥BE,
∵AH=HF,∴GH∥$\frac{1}{2}$MF,
又∵CD∥$\frac{1}{2}$BE,BE∥MF,
∴CD∥GH,
∴四边形CDHG是平行四边形,
∴CG∥DH,
又∵CG?平面ADF,DH?平面ADF,
∴CG∥平面ADF;…(4分)
(2)解:如图,以B为原点,分别以BC、BE、BA所直线为x轴、y轴、z轴建立空间直角坐标系O-xyz,
则A(0,0,2),C(1,0,0),D(1,1,0),E(0,2,0),F(0,2,1),$\overrightarrow{DE}$=(-1,1,0),
$\overrightarrow{DA}$=(-1,-1,2),$\overrightarrow{FA}$=(0,-2,1);
设平面ADF的一个法向量为$\overrightarrow{n}$=(x,y,z),则有
$\overrightarrow{n}$•$\overrightarrow{DA}$=-x-y+2z=0且$\overrightarrow{n}$•$\overrightarrow{FA}$=(=-2y+z=0,
解得:x=3y,z=2y,
令y=1得:$\overrightarrow{n}$=(3,1,2),
设直线DE与平面ADF所成的角为θ,则有sinθ=|$\frac{\overrightarrow{n}•\overrightarrow{DE}}{|\overrightarrow{n}||\overrightarrow{DE}|}$|=$\frac{\sqrt{7}}{7}$.
所以直线DE与平面ADF所成的角的正弦值为$\frac{\sqrt{7}}{7}$ …(8分)
(3)解:由已知平面ADF的法向量$\overrightarrow{m}$=(3,1,2),$\overrightarrow{BF}$=(0,2,1),
设平面BDF的一个法向量为$\overrightarrow{m}$=(x,y,z),$\overrightarrow{BD}$=(1,1,0),
由$\overrightarrow{m}$•$\overrightarrow{BF}$=2y+z=0且$\overrightarrow{m}$•$\overrightarrow{BD}$=x+y=0 解得:z=-2y,x=-y;
令y=-1得:$\overrightarrow{m}$=(1,-1,2),
设锐二面角B-DF-A的平面角为α,
则cosα=|cos<$\overrightarrow{m}$,$\overrightarrow{n}$>|=$\frac{6}{\sqrt{14}•\sqrt{6}}$=$\frac{\sqrt{21}}{7}$,
所以锐二面角B-DF-A的余弦值为$\frac{\sqrt{21}}{7}$.…(12分)
点评 本题考查线面平行的判定,直线与平面所成的角,锐二面角B-DF-A的余弦值,考查学生分析解决问题的能力,正确求出平面的法向量是关键.

 阅读快车系列答案
阅读快车系列答案
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
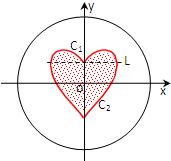 如图所示,一个圆形靶子的中心是一个“心形”图案,其中“心形”图案是由上边界C1(虚线L上方部分)与下边界C2(虚线L下方部分)围成,曲线C1是函数y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$ 的图象,曲线C2是函数y=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 的图象,圆的方程为x2+y2=8,某人向靶子射出一箭(假设此人此箭一定能射中靶子且射中靶中任何一点是等可能的),则此箭恰好命中“心形”图案的概率为( )
如图所示,一个圆形靶子的中心是一个“心形”图案,其中“心形”图案是由上边界C1(虚线L上方部分)与下边界C2(虚线L下方部分)围成,曲线C1是函数y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$ 的图象,曲线C2是函数y=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 的图象,圆的方程为x2+y2=8,某人向靶子射出一箭(假设此人此箭一定能射中靶子且射中靶中任何一点是等可能的),则此箭恰好命中“心形”图案的概率为( )| A. | $\frac{1}{4}$-$\frac{1}{18π}$ | B. | $\frac{1}{16}$-$\frac{1}{18π}$ | C. | $\frac{1}{8}$+$\frac{1}{18π}$ | D. | $\frac{1}{8}$+$\frac{36}{35π}$ |
| A. | 2i | B. | -2i | C. | 2 | D. | -2 |
| A. | y=ex | B. | y=-x | C. | y=lgx | D. | y=|x| |
| A. | {-1} | B. | {-1,1,3} | C. | {1,3} | D. | {-1,3} |