题目内容
7.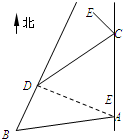 如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向用与B相距10$\sqrt{2}$ 海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.
如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向用与B相距10$\sqrt{2}$ 海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.(1)求乙船每小时航行多少海里?
(2)在C的北偏西30°方向且与C相距$\frac{8\sqrt{3}}{3}$海里处有一个暗礁E,周围$\sqrt{2}$海里范围内为航行危险区域.问:甲、乙两船按原航向和速度航行有无危险?若有危险,则从有危险开始,经过多少小时后能脱离危险?若无危险,请说明理由.
分析 (1)连接AD,CD,推断出△ACD是等边三角形,在△ABD中,利用余弦定理求得BD的值,进而求得乙船的速度.
(2)建立如图所示的坐标系,危险区域在以E为圆心,r=$\sqrt{2}$的圆内,求出E到直线BD的距离,与半径比较,即可得出结论.
解答 解:如图,连接AD,CD,由题意CD=10,AC=$\frac{20}{60}×30$=10,∠ACD=60°
∴△ACD是等边三角形,
∴AD=10,
∵∠DAB=45°
△ABD中,BD=$\sqrt{A{D}^{2}+A{B}^{2}-2AB×AD×cos45°}$=10,
∴v=10×3=30海里.
答:乙船每小时航行30海里.
(2)建立如图所示的坐标系,危险区域在以E为圆心,r=$\sqrt{2}$的圆内,直线BD的方程为y=$\sqrt{3}$x,∠DAB=∠DBA=45°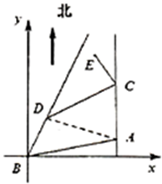
E的坐标为(ABcos15°-CEsin30°,ABsin15°+CEcos30°+AC),
求得A(5$\sqrt{3}$+5,5$\sqrt{3}$-5),C(5$\sqrt{3}$+5,5$\sqrt{3}$+5),E(5+$\frac{11\sqrt{3}}{3}$,9+5$\sqrt{3}$),
E到直线BD的距离d1=$\frac{|5\sqrt{3}+11-9-5\sqrt{3}|}{2}$=1<$\sqrt{2}$,故乙船有危险;
点E到直线AC的距离d2=$\frac{4\sqrt{3}}{3}$>$\sqrt{2}$,故甲船没有危险.
以E为圆心,半径为$\sqrt{2}$的圆截直线BD所得的弦长分别为l=2$\sqrt{{r}^{2}-{{d}_{1}}^{2}}$=2,
乙船遭遇危险持续时间为t=$\frac{2}{30}$=$\frac{1}{15}$(小时),
答:甲船没有危险,乙船有危险,且在遭遇危险持续时间$\frac{1}{15}$小时后能脱离危险.
点评 本题主要考查了解三角形的实际应用.要能综合运用余弦定理,正弦定理等基础知识,考查了综合分析问题和解决实际问题的能力.

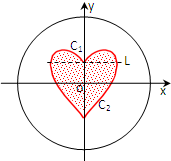 如图所示,一个圆形靶子的中心是一个“心形”图案,其中“心形”图案是由上边界C1(虚线L上方部分)与下边界C2(虚线L下方部分)围成,曲线C1是函数y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$ 的图象,曲线C2是函数y=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 的图象,圆的方程为x2+y2=8,某人向靶子射出一箭(假设此人此箭一定能射中靶子且射中靶中任何一点是等可能的),则此箭恰好命中“心形”图案的概率为( )
如图所示,一个圆形靶子的中心是一个“心形”图案,其中“心形”图案是由上边界C1(虚线L上方部分)与下边界C2(虚线L下方部分)围成,曲线C1是函数y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$ 的图象,曲线C2是函数y=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 的图象,圆的方程为x2+y2=8,某人向靶子射出一箭(假设此人此箭一定能射中靶子且射中靶中任何一点是等可能的),则此箭恰好命中“心形”图案的概率为( )| A. | $\frac{1}{4}$-$\frac{1}{18π}$ | B. | $\frac{1}{16}$-$\frac{1}{18π}$ | C. | $\frac{1}{8}$+$\frac{1}{18π}$ | D. | $\frac{1}{8}$+$\frac{36}{35π}$ |
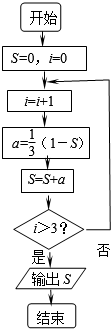
| A. | $\frac{65}{81}$ | B. | $\frac{19}{27}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{3}$ |
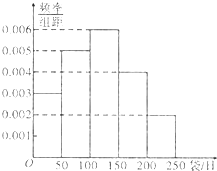 如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.