题目内容
17.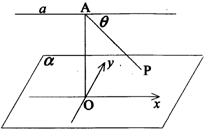 如图,已知直线a∥平面α,在平面α内有一动点P,点A是直线a上一定点,且AP与直线a所成角θ=$\frac{π}{4}$,点A到平面α的距离为2,若过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,以过点O作x轴的垂线为y轴建立直角坐标系,则动点P的轨迹方程为x2-y2=4..
如图,已知直线a∥平面α,在平面α内有一动点P,点A是直线a上一定点,且AP与直线a所成角θ=$\frac{π}{4}$,点A到平面α的距离为2,若过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,以过点O作x轴的垂线为y轴建立直角坐标系,则动点P的轨迹方程为x2-y2=4..
分析 建立坐标系,作PB⊥y轴,连接AB,设P点坐标为:(x,y),由题意可得:∠APB=θ,AB=xtanθ,OB=y,AO=d,利用勾股定理可得动点P的轨迹方程.
解答 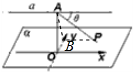 解:过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,
解:过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,
以过点O作x轴的垂线为y轴建立直角坐标系,作PB⊥y轴,连接AB,
设P点坐标为:(x,y),
由题意可得:∠APB=θ=$\frac{π}{4}$,AB=xtanθ=x,OB=y,AO=d=2.
所以,由勾股定理可得:(xtanθ)2=d2+y2,即:x2=22+y2,
整理可得动点P的轨迹方程为:x2-y2=4.
故答案为:x2-y2=4.
点评 本题主要考查了勾股定理,求动点的轨迹方程,考查了空间想象能力和转化思想,属于基本知识的考查.

练习册系列答案
相关题目
8.若直线l:mx+ny=4和圆O:x2+y2=4没有交点,则过点(m,n)的直线与椭圆$\frac{x^2}{9}+\frac{y^2}{4}=1$的交点个数为( )
| A. | 0个 | B. | 至多有一个 | C. | 1个 | D. | 2个 |
2.已知函数f(x)=loga(x+1)(a>0,a≠1)在[0,1]上的值域是[0,1],若函数g(x)=ax-m-4的图象不过第二象限,则m的取值范围是( )
| A. | [-2,+∞) | B. | [-$\frac{1}{2}$,+∞) | C. | [-1,+∞) | D. | (-∞,2] |
9.设集合A={x|x2-x-2≤0},B={x|x≥a+1},若A?B,则a的取值范围是( )
| A. | a<2 | B. | a≥-2 | C. | a≤-2 | D. | a>2 |
7.设a∈[0,4],则使方程x2+ax+1=0有解的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |