题目内容
5.已知i为虚数单位,复数z满足(1+2i)z=1-2i,则复数z=-$\frac{3}{5}$$-\frac{4}{5}i$.分析 直接利用复数的代数形式的混合运算,化简求解即可.
解答 解:因为(1+2i)z=1-2i,
所以z=$\frac{1-2i}{1+2i}$=$\frac{(1-2i)(1-2i)}{(1+2i)(1-2i)}$=$\frac{-3-4i}{5}$=-$\frac{3}{5}$$-\frac{4}{5}i$.
故答案为:-$\frac{3}{5}$$-\frac{4}{5}i$.
点评 本题考查复数的代数形式的混合运算,基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.函数y=f(x)图象如图所示,则函数的单调减区间为( )


| A. | [-3,3] | B. | [-1,2] | C. | [-3,-1] | D. | [2,3] |
1.椭圆$\frac{x^2}{4}+\frac{y^2}{m}=1$的焦距为2,则m的值为( )
| A. | 3 | B. | $\sqrt{15}$ | C. | 3或5 | D. | 3或$\sqrt{15}$ |
2.已知函数f(x)=loga(x+1)(a>0,a≠1)在[0,1]上的值域是[0,1],若函数g(x)=ax-m-4的图象不过第二象限,则m的取值范围是( )
| A. | [-2,+∞) | B. | [-$\frac{1}{2}$,+∞) | C. | [-1,+∞) | D. | (-∞,2] |
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2,PD⊥底面ABCD,E为棱PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2,PD⊥底面ABCD,E为棱PC的中点.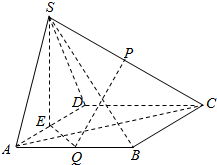 如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.
如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.