题目内容
已知点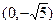 是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为
是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为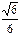 ,椭圆的左右焦点分别为F1和F2 。
,椭圆的左右焦点分别为F1和F2 。
(Ⅰ)求椭圆方程;
(Ⅱ)点M在椭圆上,求⊿MF1F2面积的最大值;
(Ⅲ)试探究椭圆上是否存在一点P,使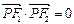 ,若存在,请求出点P的坐标;若不存在,请说明理由。
,若存在,请求出点P的坐标;若不存在,请说明理由。
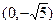 是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为
是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为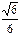 ,椭圆的左右焦点分别为F1和F2 。
,椭圆的左右焦点分别为F1和F2 。(Ⅰ)求椭圆方程;
(Ⅱ)点M在椭圆上,求⊿MF1F2面积的最大值;
(Ⅲ)试探究椭圆上是否存在一点P,使
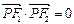 ,若存在,请求出点P的坐标;若不存在,请说明理由。
,若存在,请求出点P的坐标;若不存在,请说明理由。(Ⅰ)
(Ⅱ)
(Ⅲ)不存在,理由见解析。

(Ⅱ)

(Ⅲ)不存在,理由见解析。
(Ⅰ)设椭圆方程为 ,由已知,
,由已知,
 ,
,  . 解得
. 解得 ,
,
∴所求椭圆方程为 。
。
(Ⅱ)令 ,则
,则
∵ ,故
,故 的最大值为
的最大值为 ,
,
∴当 时,
时, 的最大值为
的最大值为 。
。
(Ⅲ)假设存在一点P, 使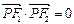 ,
, ∴
∴ ,∴⊿PF1F2为直角三角形,∴
,∴⊿PF1F2为直角三角形,∴ ①,
①,
又∵ ②,
②,
∴②2-①,得 ∴
∴
即 =5,但由(1)得
=5,但由(1)得 最大值为
最大值为 ,故矛盾,
,故矛盾,
∴不存在一点P, 使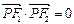 。
。
 ,由已知,
,由已知,
 ,
,  . 解得
. 解得 ,
,∴所求椭圆方程为
 。
。(Ⅱ)令
 ,则
,则
∵
 ,故
,故 的最大值为
的最大值为 ,
,∴当
 时,
时, 的最大值为
的最大值为 。
。(Ⅲ)假设存在一点P, 使
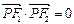 ,
, ∴
∴ ,∴⊿PF1F2为直角三角形,∴
,∴⊿PF1F2为直角三角形,∴ ①,
①,又∵
 ②,
②,∴②2-①,得
 ∴
∴
即
 =5,但由(1)得
=5,但由(1)得 最大值为
最大值为 ,故矛盾,
,故矛盾,∴不存在一点P, 使
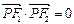 。
。
练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 =
= ,
,  =
= ,求
,求 ,
, 及
及 的值
的值

 有相同的焦点,且椭圆过点
有相同的焦点,且椭圆过点 ,
, 过点
过点 交椭圆于
交椭圆于 两点,且
两点,且 ,求直线
,求直线 ,曲线
,曲线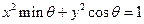 和
和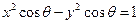 有4个不同的交点.
有4个不同的交点.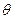 的取值范围;
的取值范围;
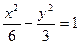 的渐近线与圆
的渐近线与圆 相切,则r=
相切,则r=
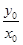 的取值范围为________.
的取值范围为________. 的方程为
的方程为
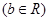 ,则直线
,则直线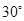
 有关
有关