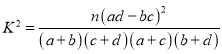题目内容
【题目】某公司印制了一批文化衫,每件文化衫可有红、黄、蓝三种不同的颜色和四种不同的图案.现将这批文化衫分发给![]() 名新员工,每名员工恰好分到图案不同的4件.试求
名新员工,每名员工恰好分到图案不同的4件.试求![]() 的最小值,使得总存在两个人,他们所分到的某两种图案的4件文化衫的颜色全部相同.
的最小值,使得总存在两个人,他们所分到的某两种图案的4件文化衫的颜色全部相同.
【答案】19
【解析】
![]() 的最小值为19.
的最小值为19.
当![]() 时,表1所示的答题情形不符合要求.
时,表1所示的答题情形不符合要求.
表1
|
|
|
|
|
|
|
|
|
|
|
|
| p> |
|
|
|
| |
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【注】表l中(1)、(2)、(3)、(4)为图案,![]() 为员工,
为员工,![]() 、
、![]() 、
、![]() 分别表示红、黄、蓝三种颜色.
分别表示红、黄、蓝三种颜色.
下面证明:当![]() 时,必存在两个人满足要求.
时,必存在两个人满足要求.
事实上,把所有人的文化衫的颜色和图案如上制成表格,若存在两个人的某两种图案的4件文化衫的颜色全部相同,则必存在一个矩形子表,这个子表四个角的方格中的字母(颜色)相同.
若对于某个颜色(以红色为例),设![]() 分到
分到![]() 件红色文化衫.则当
件红色文化衫.则当![]() 时(约定当
时(约定当![]() 时,
时,![]() ),必存在四个角都是
),必存在四个角都是![]() 的矩形.这是因为,考虑每一列两个
的矩形.这是因为,考虑每一列两个![]() 构成的“对子”,一共只有如表2所示的6种.当
构成的“对子”,一共只有如表2所示的6种.当![]() 时,必有两列会出现相同的对子,从而,必有四个角都是
时,必有两列会出现相同的对子,从而,必有四个角都是![]() 的矩形.
的矩形.
表2
|
|
| |||
|
|
| |||
|
|
| |||
|
|
|
当![]() 时,任取其中19个人,他们的所有文化衫的颜色中,至少有一种颜色出现了不少于
时,任取其中19个人,他们的所有文化衫的颜色中,至少有一种颜色出现了不少于![]() (次),不妨设为红色.
(次),不妨设为红色.
设其中![]()
![]() (
(![]() 为非负整数)件红色文化衫.则
为非负整数)件红色文化衫.则![]() .
.
由调整法易知,当![]() 取最小值时,对任意
取最小值时,对任意![]() ,有
,有![]() .
.
注意到![]() ,则在
,则在![]() 中有19个1和7个2时,
中有19个1和7个2时,![]() 取得最小值
取得最小值![]() .
.
这表明,当![]() 时,必存在四个角都是同一个字母的矩形子表.
时,必存在四个角都是同一个字母的矩形子表.
综上,所求![]() 的最小值为19.
的最小值为19.

【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取100人做调查,得到![]() 列联表,且已知在100个人中随机抽取1人,抽到喜欢游泳的学生的概率为
列联表,且已知在100个人中随机抽取1人,抽到喜欢游泳的学生的概率为![]() .
.
(1)请完成![]() 列联表;
列联表;
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 100 |
(2)根据列联表,是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由.
附:参考公式与临界值表如下:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |