Question

【题目】已知函数f(x)＝|3x＋2|.

(1)解不等式f(x)<4－|x－1|；

(2)已知m＋n＝1(m，n>0)，若|x－a|－f(x)≤(a>0)恒成立，求实数a的取值范围.

Answer 1

【答案】(1)；(2).

【解析】

（1）利用零点分段法分类讨论解绝对值不等式即可.

（2）利用基本不等式求出的最小值，令g(x)＝|x－a|－f(x)＝|x－a|－|3x＋2|，只需g(x)max即可求解.

(1)不等式f(x)<4－|x－1|，即|3x＋2|＋|x－1|<4.

当x<－时，即－3x－2－x＋1<4，

解得－<x<－；

当－≤x≤1时，即3x＋2－x＋1<4，

解得－≤x<；

当x>1时，即3x＋2＋x－1<4，无解．

综上所述，不等式的解集为.

(2) ＝ (m＋n)＝1＋1＋，

当且仅当时取等号，

令g(x)＝|x－a|－f(x)＝|x－a|－|3x＋2|＝，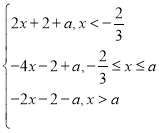

所以当x＝－时，g(x)max＝＋a，要使不等式恒成立，

只需g(x)max＝＋a≤4，即0<a≤

.故实数a的取值范围为.