已知某几何体的三视图如图所示.则该几何体的体积为11．题目和参考答案——青夏教育精英家教网—

题目内容

15．已知某几何体的三视图如图所示，则该几何体的体积为11．

分析根据几何体的三视图，及其数据得出几何体，利用体积公式求解即可．

解答解：根据几何体的三视图，及其数据得出：AD=2，AB=2，AA₁=3，O为A₁B₁中点，
几何体是长方体截去一个角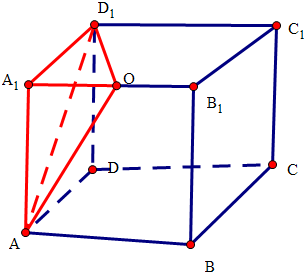

∴该几何体的体积为2×2×3$-\frac{1}{3}×\frac{1}{2}×2×1×3$=12-1=11．
故答案为：11．

点评本题考查了空间几何体的三视图，运用恢复直观图，求解体积，考查了空间想象能力，计算能力．

练习册系列答案

-$\frac{\sqrt{3}}{3}$

6．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=$\sqrt{3}$，$\overrightarrow{a}+\overrightarrow{b}$=（$\sqrt{3}$，1），求：
（1）|$\overrightarrow{a}-\overrightarrow{b}$|；
（2）$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}-\overrightarrow{b}$的夹角．

3．在△ABC中，若∠A=60°，a=1，求△ABC内切圆半径R的最大值．

10．已知f（x）=3-2|x|，g（x）=x²-2x，F（x）=min{f（x），g（x）}，则F（x）的最值是（　　）

	A．	最大值为3，最小值为-1		B．	最大值为7-2$\sqrt{7}$，无最小值
	C．	最大值为3，无最小值		D．	既无最大值，也无最小值

20．

如图，梯形ABCD中，AD∥BC，DC⊥BC，AD=2，BC=6，若以AB为直径的⊙O与CD相切于点E，则DE等于（　　）

7．在△ABC中，角A，B，C的对边分别为a，b，c，且bcosC=（2a-c）cosB．
（Ⅰ）求角B的大小；
（Ⅱ）若a，b，c成等差数列，且b=3，试求△ABC的面积．

4．下列函数中，既是奇函数，又在（-∞，+∞）上为增函数的是（　　）

5．已知向量$\overrightarrow{a}$=（cosθ，-2），$\overrightarrow{b}$=（sinθ，1），且$\overrightarrow{a}$∥$\overrightarrow{b}$，则tan（θ-$\frac{π}{4}$）等于（　　）

试题分类