题目内容
10.已知f(x)=3-2|x|,g(x)=x2-2x,F(x)=min{f(x),g(x)},则F(x)的最值是( )| A. | 最大值为3,最小值为-1 | B. | 最大值为7-2$\sqrt{7}$,无最小值 | ||
| C. | 最大值为3,无最小值 | D. | 既无最大值,也无最小值 |
分析 先根据函数f(x)、g(x)的解析式画出函数图象,求出交点,再根据函数F(x)的定义画出其图象,再根据图象可求出函数的最大值和最小值.
解答 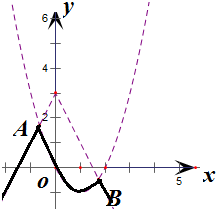 解:∵函数f(x)=3-2|x|,g(x)=x2-2x,
解:∵函数f(x)=3-2|x|,g(x)=x2-2x,
∴函数F(x)的图象如图,
联立方程组$\left\{\begin{array}{l}{y=3+2x}\\{y={x}^{2}-2x}\\{x<0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2-\sqrt{7}}\\{y=7-2\sqrt{7}}\end{array}\right.$,
即A(2-$\sqrt{7}$,7-2$\sqrt{7}$),
结合函数图象可知函数F(x)有最大值7-2$\sqrt{7}$,无最小值,
故选:B.
点评 本题考查函数的图象以及函数求最值,同时考查了分析问题的能力和作图的能力,注意解题方法的积累,属于中档题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
5.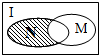 设全集是实数集R,M={x|x>2}与N={x|1<x≤3}都是R的子集(如图所示),则阴影部分所表示的集合为( )
设全集是实数集R,M={x|x>2}与N={x|1<x≤3}都是R的子集(如图所示),则阴影部分所表示的集合为( )
 设全集是实数集R,M={x|x>2}与N={x|1<x≤3}都是R的子集(如图所示),则阴影部分所表示的集合为( )
设全集是实数集R,M={x|x>2}与N={x|1<x≤3}都是R的子集(如图所示),则阴影部分所表示的集合为( )| A. | {x|1<x≤2} | B. | {x|x<2} | C. | {x|-2≤x<1} | D. | {x|-2≤x≤2} |
2.已知命题p:对于?x∈R,恒有2x+2-x≥2成立,命题q:奇函数f(x)的图象必过原点.则下列结论正确的是( )
| A. | p∧q为真 | B. | (?p)∨q为真 | C. | p∧(?q)为真 | D. | ?p为真 |
19.阅读如图所示的程序框图,运行相应的程序,若输入x的值为-5,则输出y的值为( )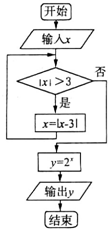

| A. | 0.5 | B. | 1 | C. | 2 | D. | 4 |
20.已知集合A={x|y=$\sqrt{\frac{x-1}{x-4}}$},B={y|y=$\sqrt{16-{2}^{x}}$},则A∩B=( )
| A. | [1,4] | B. | [1,4) | C. | [0,1] | D. | (0,4) |
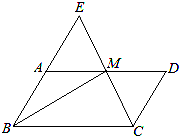 已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证:
已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证: