题目内容
某种产品按质量标准分成五个等级,等级编号依次为1,2,3,4,5.现从一批产品中随机抽取20件,对其等级编号进行统计分析,得到频率分布表如下:
| 等级 | 1 | 2 | 3 | 4 | 5 |
| 频率 | a | 0.2 | 0.45 | b | c |
(2)在(1)的条件下,将等级编号为4的3件产品记为xl,x2,x3,等级编号为5的2件产品记为yl ,y2,现从xl,x2,x3,yl,y2这5件产品中任取两件(假定每件产品被取出的可能性相同),写出所有可能的结果,并求这两件品的级编号恰好相同的概率。
(1)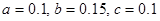 ;(2)
;(2)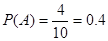 。
。
解析试题分析:(1)由频率分布表得 2分
2分
因为抽取的20件产品中,等级编号为4的恰有3件,所以
等级编号为5的恰有2件,所以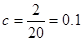 4分
4分
从而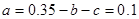 . 所以
. 所以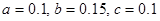 6分
6分
(2)从产品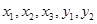 中任取两件,所有可能的结果为:
中任取两件,所有可能的结果为: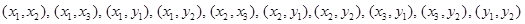
共10种 8分
设事件A表示“从产品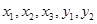 中任取两件,其等级编号相同”,则A包含的基本事件为:
中任取两件,其等级编号相同”,则A包含的基本事件为: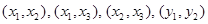 共4种 10分
共4种 10分
故所求的概率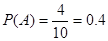 12分
12分
考点:本题主要考查频率分布表,频率的概念及计算,古典概型概率的计算。
点评:典型题,统计中的抽样方法,频率分布表,概率计算及分布列问题,是高考必考内容及题型。古典概型概率的计算问题,关键是明确基本事件数,往往借助于“树图法”,做到不重不漏。

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 ,且他们是否译出密码互不影响。
,且他们是否译出密码互不影响。
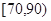 段的有多少人;
段的有多少人; 次,每次投篮的结果相互独立.在
次,每次投篮的结果相互独立.在 处每投进一球得
处每投进一球得 处每投进一球得
处每投进一球得 分,否则得
分,否则得 分. 将学生得分逐次累加并用
分. 将学生得分逐次累加并用 表示,如果
表示,如果 ,在
,在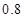 .
. ;
; ,
, ,
, ,
, ,
, ,
, .
. ,出现绿灯的概率都是
,出现绿灯的概率都是 .记这4盏灯中出现红灯的数量为
.记这4盏灯中出现红灯的数量为 ,当这排装饰灯闪烁一次时:
,当这排装饰灯闪烁一次时: 时的概率;(2)求
时的概率;(2)求 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
. ,求
,求 ,求
,求