题目内容
(本小题满分12分)某班从6名班干部中(男生4人,女生2人)选3人参加学校义务劳动;(1)求男生甲或女生乙被选中的概率;
(2)在男生甲被选中的情况下,求女生乙也被选中的概率;
(3)设所选3人中女生人数为 ,求
,求 的分布列及数学期望。
的分布列及数学期望。
(1) ;(2)
;(2)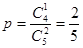 ;
;
(3)
0 1 2 
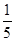
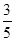
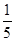
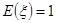
解析试题分析:(1) ……………………………………………………………4分
……………………………………………………………4分
(2)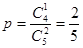 ………………………………………………………………….……..8分
………………………………………………………………….……..8分
(3)
0 1 2 
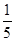
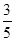
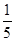
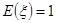 ………………………………………………………………… ………..12分
………………………………………………………………… ………..12分
考点:离散型随机变量的期望与方差;等可能事件的概率。
点评:本题主要考查等可能事件的概率与离散型随机变量的分布列、期望与方差等知识点,属于中档题型,高考命题的趋向.分布列的求解应注意以下几点:(1)弄清随机变量每个取值对应的随机事件;(2)计算必须准确无误;(3)注意用分布列的两条性质检验所求的分布列是否正确。

练习册系列答案
相关题目
某种产品按质量标准分成五个等级,等级编号依次为1,2,3,4,5.现从一批产品中随机抽取20件,对其等级编号进行统计分析,得到频率分布表如下:
| 等级 | 1 | 2 | 3 | 4 | 5 |
| 频率 | a | 0.2 | 0.45 | b | c |
(2)在(1)的条件下,将等级编号为4的3件产品记为xl,x2,x3,等级编号为5的2件产品记为yl ,y2,现从xl,x2,x3,yl,y2这5件产品中任取两件(假定每件产品被取出的可能性相同),写出所有可能的结果,并求这两件品的级编号恰好相同的概率。
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中的微量元素 ,
, 的含量(单位:毫克)下表是乙厂的5件产品的测量数据:
的含量(单位:毫克)下表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
 | 160 | 178 | 166 | 175 | 180 |
 | 75 | 80 | 77 | 70 | 81 |
(2)若
 且
且 为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数
为次品,从乙厂抽出的上述5件产品中,有放回的随机抽取1件产品,抽到次品则停止抽取,否则继续抽取,直到抽出次品为止,但抽取次数最多不超过3次,求抽取次数 的分布列及数学期望.
的分布列及数学期望. (本小题满分12分)
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在8,9,10环,且每次射击击中与否互不影响.甲、乙射击命中环数的概率如表:
| | 8环 | 9环 | 10环 |
| 甲 | 0.2 | 0.45 | 0.35 |
| 乙 | 0.25 | 0.4 | 0.35 |
(Ⅱ)若甲、乙两运动员各自射击2次,求这4次射击中恰有3次击中9环以上(含9环)的概率.
 ,求:
,求: 上的概率;
上的概率;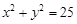 外的概率。
外的概率。 是锐角三角形的概率。
是锐角三角形的概率。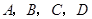 四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加
四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加 岗位服务的概率;(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;(Ⅲ)设随机变量
岗位服务的概率;(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;(Ⅲ)设随机变量 为这五名志愿者中参加
为这五名志愿者中参加 中,平面区域
中,平面区域 中的点的坐标
中的点的坐标 满足
满足 ,从区域
,从区域 .
. ,
, ,求点
,求点 位于第四象限的概率;
位于第四象限的概率; 与圆
与圆 相交所截得的弦长为
相交所截得的弦长为 ,求
,求 的概率.
的概率.