题目内容
在平面 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
.
(1)定义横、纵坐标为整数的点为“整点”. 在区域 中任取3个“整点”,求这些“整点”中恰好有2个“整点”落在区域
中任取3个“整点”,求这些“整点”中恰好有2个“整点”落在区域 中的概率;
中的概率;
(2)在区域 中每次任取一个点,连续取3次,得到3个点,记这3个点落在区域
中每次任取一个点,连续取3次,得到3个点,记这3个点落在区域 中的个数为
中的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(1) (2)
(2) 的分布列为
的分布列为
0 1 2 3 

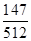


∴ 的数学期望:
的数学期望: .
.
解析试题分析:(1)依题可知平面区域 的整点为:
的整点为: 共有13个,上述整点在平面区域
共有13个,上述整点在平面区域 内的为:
内的为: 共有3个,
共有3个,
∴ .
.
(2)依题可得,平面区域 的面积为
的面积为 ,设扇形区域中心角为
,设扇形区域中心角为 ,则
,则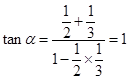 得
得 ,平面区域
,平面区域 与平面区域
与平面区域 相交部分的面积为
相交部分的面积为 .
.
在区域 任取1个点,则该点在区域
任取1个点,则该点在区域 的概率为
的概率为 ,随机变量
,随机变量 的可能取值为:
的可能取值为: .
. ,
,  ,
, ,
,  ,
,
∴ 的分布列为
的分布列为
0 1 2 3 

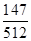


∴ 的数学期望:
的数学期望: .
.
考点:古典概型概率及分布列期望
点评:古典概型概率的求解先要找到所有基本事件总数及满足题意要求的基本事件种数,然后求其比值;分布列的题目要根据题目所描述的问题找到随机变量可取的值,再依次求出各值对应的概率列表即可

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
某种产品按质量标准分成五个等级,等级编号依次为1,2,3,4,5.现从一批产品中随机抽取20件,对其等级编号进行统计分析,得到频率分布表如下:
| 等级 | 1 | 2 | 3 | 4 | 5 |
| 频率 | a | 0.2 | 0.45 | b | c |
(2)在(1)的条件下,将等级编号为4的3件产品记为xl,x2,x3,等级编号为5的2件产品记为yl ,y2,现从xl,x2,x3,yl,y2这5件产品中任取两件(假定每件产品被取出的可能性相同),写出所有可能的结果,并求这两件品的级编号恰好相同的概率。
 ,乙射击一次中靶概率是
,乙射击一次中靶概率是 ,
, ,求
,求 ,求:
,求: 上的概率;
上的概率;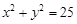 外的概率。
外的概率。 是锐角三角形的概率。
是锐角三角形的概率。